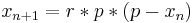Från Rilpedia

Den här artikeln anses vara otydlig eller onödigt fackspråklig. Hjälp gärna till att förtydliga artikeln och göra den mer lättläst. Se eventuellt diskussionssidan för mer information.

Ett bifurkationsdiagram är en grafisk representation av hur en viss population konvergerar då tillväxthastigheten varierar och då iterationen låts gå mot oändligheten, där populationens nästkommande värde kan uttryckas som en funktion av föregående iterations värde.

En sådan population har ofta en formel med detta utseende:

där x_n är det tillfälliga värdet, x_{n + 1} nästa iterations värde och r är populationens tillväxthastighet för en iteration; exempelvis skulle r = 2 innebära en fördubbling och r = 3 en trefördubbling. Denna population kan variera mellan 0, som är total utrotning, och 1 som är det absoluta maximumet för populationen.

I diagrammet till höger ses tillväxthastigheten r på x-axeln och på y-axeln populationens gränsvärde(n) efter ett stort antal iterationer.

Exempelvis skulle vi kunna se formeln som ett uttryck för en viss djurarts årliga tillväxt där r är tillväxthastigheten och n är år efter ett bestämt begynnelsen. Eftersom en djurpopulation inte kan bli hur stor som helst, då exempelvis mattillgångar, yta och konkurrens spelar in, måste också en begränsande faktor, (1 − x_n) tilläggas, det vill säga om populationen är 0,4 så är överlevnaden endast 60 %. Man kan därav se att faktorn r låter populationen öka medan (1 − x_n) samtidigt skär ner den.

Om man studerar denna population och låter r variera och n gå mot oändligheten inser vi att olika saker händer beroende på val av r:

• För 0 < r < 1 kommer givetvis populationen att gå under då populationen avtar snabbare än vad den ökar.
• För 1 < r < 3 ungefär kommer populationen att konvergera mot ett visst värde, det vill säga populationen når ett stabilt läge.
• Vid r omkring 3 kommer någonting konstigt att hända, grafen delar upp sig i två spår. Detta beror på att populationen hamnar i en regelbunden svängning mellan två gränsvärden. Efter ett bra år följer ett dåligt år och därefter kommer ett bra år igen osv.
• Vid 3,5 delar sig grafen ytterligare och vi får förgreningar i potensen två, 2, 4, 8, 16 och så vidare.
• När r närmar sig 3,57 övergår grafen till ett kaotiskt tillstånd. Det uppstår inga gränsvärden utan populationen tilltar helt slumpartat. Dock uppstår emellanåt korta stunder då diagrammet återgår till att vara stabilt, vilket i diagrammet framträder som vita spalter.