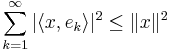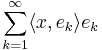Bessels olikhet

Från Rilpedia

Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif

Bessels olikhet är inom matematik, speciellt funktionalanalys, en olikhet som beskriver hur element i Hilbertrum förehåller sig till ortonormala följder.

Om H är ett Hilbertrum och e1,e2,e3,... en ortonormal följd i H, så gäller det att för alla x i H att:

\sum_{k=1}^\infty |\langle x, e_k \rangle|^2 \leq \| x \|^2

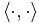där \langle \cdot , \cdot \rangle är den inre produkten. Bessels olikhet ger att summan

\sum_{k=1}^\infty \langle x, e_k \rangle e_k

konvergerar.


Lebesgue Icon.svg Denna artikel om matematisk analys är bara påbörjad. Du kan hjälpa till genom att utöka den.
Hämtad från "https://sv.rilpedia.org/wiki/Bessels_olikhet"
Personliga verktyg