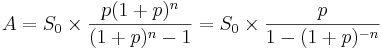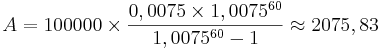Annuitetslån
Från Rilpedia
Denna artikel handlar om låneformen. För metoden för investeringskalkylering, se annuitetsmetoden.
Annuitetslån är en låneform där låntagaren periodiskt erlägger ett fast belopp, annuitet eller annuitetsbelopp, för ränta och amortering tillsammans. Till skillnad från andra låneformer så varierar inte utgiften för avbetalningar och lånekostnader över lånets löptid.

Eftersom annuiteten är konstant, så varierar däremot amorteringsdelen över löptiden. Som för alla låneformer med återkommande avbetalningar, så minskar räntekostnaden efter hand, i takt med att det räntegrundande lånebeloppet sjunker. Amorteringsdelen stiger därmed för varje betalning.
En konsekvens av detta blir att skulden inte minskar linjärt, som vid rak amortering. Istället minskar skulden långsamt i början, men allt snabbare efter hand. Den sammanlagda räntekostnaden under lånets hela löptid blir därför högre, även om skillnaden kan vara liten vid korta lån.
En annan konsekvens är att utgifterna under början av lånets löptid är lägre. Det kan gynna låntagare som har ansträngd likviditet under denna period. Det kan även medföra att låntagaren har råd med ett större lån.
För en jämförelse med andra låneformer, se Amortering.
Innehåll |
Beräkningar
En annuitetsberäkning kan endast genomföras vid fast ränta och fastställd löptid. Det är en beräkning av det fasta belopp som skall erläggas under ett antal perioder (månadsvis, kvartalsvis, halvårsvis och så vidare) för att det ursprungliga kapitalet (eller del av detta kapital) skall vara återbetalat vid den sista betalningen.
Metoden är nära besläktad med en nuvärdesberäkning. Den används även inom företagsekonomisk finansieringskalkyl, och kallas då annuitetsmetoden. Istället för begreppen lånebelopp och räntesats nedan, används då investeringskostnad och internränta.
För att beräkna annuiteten (A) behövs:
- S0 = Lånebelopp. Skuld vid löptidens början.
- p = Räntesats för perioden. En årsränta måste delas med antalet betalningsperioder per år (12 för månader, 4 för kvartal, etc). En årsränta på 9% ger alltså en månatlig räntesats på 0,0075 (=0,75% = 9%/12).
- n = Antal betalningar under lånets löptid. Månatlig amortering ger 60 (=12*5) betalningar för ett lån på fem år.
För att beräkna annuiteten i bildexemplet till höger, 100 000 kr till 9% årsränta över 5 år, blir alltså beräkningen:
Ovanstående formel utgår ifrån att alla betalningsperioder är lika långa. I verkligheten kan kan detta behöva justeras för den första, och eventuellt även den sista, perioden, om någon eller båda av dessa inte överensstämmer med den kalkylerade.
Formeln gäller då betalning sker i slutet av varje period. Kalkylen påverkas av om periodbeloppet erläggs i början eller i slutet av perioden. Vid betalning i början av perioden utgör den första betalningen endast en amortering eftersom ingen ränta ännu hunnit utgå. S0 kan i sådana fall räknas ner med en amortering.
Om räntesatsen ändras under lånets löptid, måste periodbeloppet omräknas om återbetalning skall ske inom överenskommen tid. Om periodbeloppet inte räknas om, måste tiden för återbetalning i stället justeras.
Kalkylprogram
I kalkylprogram finns det ofta en färdig funktion för beräkningen av annuitetsbeloppet. I de svenska versionerna av Microsoft Excel och OpenOffice.org Calc heter denna funktion BETALNING. Det finns även en metod för att beräkna amorteringsdelen av annuiteten för en given period, AMORT. Resultatet av dessa är negativt.
BETALNING(räntesats;löptid;lånebelopp) AMORT(räntesats;period;löptid;lånebelopp)
Löptiden ska i båda fallen ovan anges i antal perioder. Räntesatsen är per period.
Se även
Externa länkar
Referenser
Webbkällor
- ”bankir.nu - Uppslagsbok Ordlexikon”. http://www.bankir.nu/uppslagsbok/annuitet_annuitetslaan.html. Läst 25 maj 2008.
Tryckta Källor
- Malmström, Sten; Iréne Györky, Peter A. Sjögren: Bonniers svenska ordbok, Albert Bonniers Förlag AB, Stockholm [1980] 2002, 8:e uppl. (svenska). ISBN 91-0-057704-9.