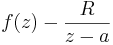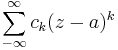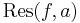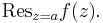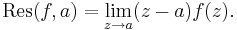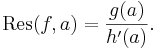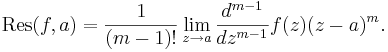Residy
Från Rilpedia
En residy är inom komplex analys ett tal som beskriver beteendet hos kurvintegraler av meromorfa funktioner runt en singulär punkt. Residyer är relativt lättberäknade och kan användas till att bestämma avancerade integraler via residysatsen.
Definition
Residyn av en meromorf funktion f vid en isolerad singularitet a är det entydigt bestämda komplexa talet R så att funktionen
har en anlytisk primitiv funktion i den punkterade skivan 0 < | z − a | < δ
Residyn vid a kan även definieras som termen c − 1 i Laurentutvecklingen av f(z) kring a:
Residyn av funktionen f i punkten a betecknas vanligen
eller
Beräkning
Om f är analytisk i a, så
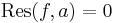 .
.
Om f har en enkel pol i a kan residyn beräknas med:
Om g och h är analytiska och f(z) = g(z) / h(z) har en enkel pol i a fås residyn av:
Generellt, om f har en pol av ordning m i punkten a:
Man kan även beräkna funktionens Laurentserie och läsa av koefficienten c − 1.
Referenser
- Ahlfors, Lars: Complex Analysis, McGraw-Hill, 1979. ISBN 0-07-000657-1.
- Saff, E.B.; A.D. Snider: Fundamentals of Complex Analysis, Prentice Hall, 2003. ISBN 0-13-017968-X.