Principalkomponentanalys

Från Rilpedia

Texten från svenska Wikipedia

PCA står för principal component analysis och är en metod för att reducera antalet dimensioner i data, för att lättare hitta samband eller för visualisering. PCA väljer ut ett nytt koordinatsystem av lägre dimension och behåller så mycket variansen på datan som möjligt, samtidigt som komponenterna är vinkelräta och datan kommer inte att ha någon kovarians i det nya koordinatsystemet.

Låt x vara en n-dimensionell vektor med attribut, till exempel från ett bildigenkänningsproblem. x skulle kunna bestå av tre färgvärden för en pixel. Samla N > n exempel på x, till exempel från alla pixlar i en given bild.

Utför korrelationsanalys, dvs beräkna kovariansmatrisen C av datan. PCA är nu att hitta en linjär transform av data så att kovariansmatrisen blir diagonal, dvs i vilka riktningar data varierar mest. De riktningarna kallas principalkomponenter eller principalaxlar. Detta görs genom att linjärisera kovariansmatrisen.

Punkter i två dimensioner

De två första komponenterna av samma punkter efter PCA

Olinjär PCA

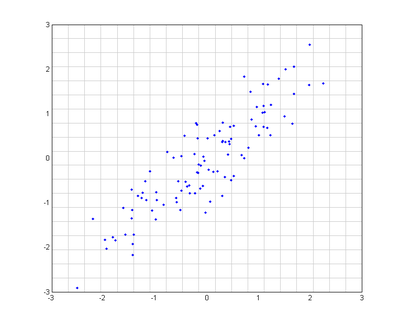
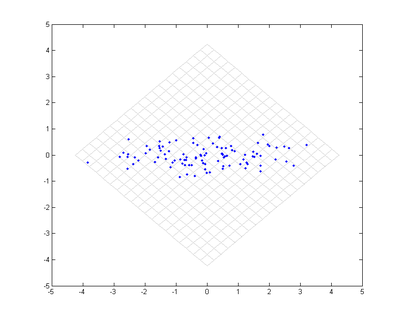
Genom att formulera PCA endast uttryckt i skalärprodukter kan man hitta principalkomponenter i rum av mycket högre dimension än den ursprungliga datan, utan att beräkna vektorerna i detta rum explicit.^[1] Figurerna visar ett exempel på detta. Färgerna på punkterna och rutnätet är bara till för att bättre illustrera metoded; de har ingen betydelse för algoritmen. Kärnan som användes var Gaussisk, dvs 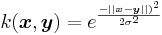. Kärnan är skalärprodukten av de två vektorerna i R2 av högre dimension.

Punkter i två dimensioner

De två första komponenterna av samma punkter efter olinjär PCA med en Gaussisk kärna.

Referenser

1. ↑ Nonlinear Component Analysis as a Kernel Eigenvalue Problem (PDF) En bra beskrivning av hur kärnor kan användas till att genomföra olinjär PCA

Externa länkar

• A Tutorial on Principal Component Analysis (PDF)
• A tutorial on PCA by Lindsay I. Smith (PDF)