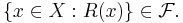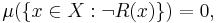Nästan överallt

Från Rilpedia

Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif

Nästan överallt är ett matematiskt begrepp. Om något gäller nästan överallt, gäller det överallt utom på en nollmängd, vilket är en mängd med måttet 0.

Exempel

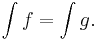  • Om två funktioner är lika nästan överallt så är alla integraler över funktionerna lika. Med andra ord, om f och g är lika nästan överallt så är \int f = \int g..
  • Om vi använder det vanliga Lebesguemåttet så är nästan alla reella tal irrationella.

Formell definition

Låt 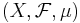(X,\mathcal{F},\mu) vara ett måttrum och 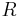R\, ett mätbart predikat i 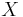X\,, dvs mängden

\{x \in X : R(x)\} \in \mathcal{F}.

Man säger att 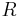R\, gäller µ-nästan överallt i 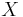X\, om och endast om

\mu(\{x \in X : \neg R(x) \}) = 0,

dvs den mängden där predikatet 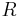R\, inte stämmer är en µ-nollmängd.

Se även

Hämtad från "https://sv.rilpedia.org/wiki/N%C3%A4stan_%C3%B6verallt"
Personliga verktyg