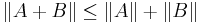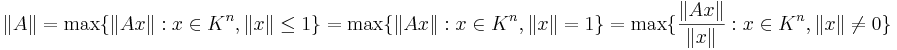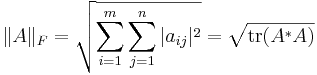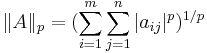Matrisnorm
Från Rilpedia
Inom matematik är en matrisnorm en naturlig förlängning av vektorrnormen för matriser.
Innehåll |
Egenskaper
En matrisnorm har samma egenskaper som en vektornorm, och följande gäller då för en matrisnorm i rummet Km,n, då K är en kropp, t.ex. de reella eller komplexa talen. A och B är matriser i Km,n:
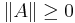 med likhet om och endast om A = 0
med likhet om och endast om A = 0
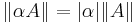 för alla
för alla 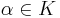
Inducerade normer
Om normer för Km och Kn är givna (då K är någon kropp, exempelvis de reella eller komplexa talen), kan man definiera en inducerad norm (en så kallad operatornorm) på rummet av alla matriser med format m × n med:
Om vektornormen är en p-norm blir då matrisnormen:
Om p = 1 eller 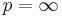 kan normen beräknas som:
kan normen beräknas som:

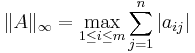 .
.
Om p = 2 och m = n kallas den inducerade matrisnormen för spektralnormen och är lika med matrisens största singulärvärde eller den roten ur det största egenvärdet till den positivt definita matrisen A * A:
 ,
,
där A * är det hermiteska konjugatet till A.
Elementvisa normer
För matriser i Km,n:
Frobeniusnormen
Frobeniusnormen är i princip en förlänging av den vanliga euklidiska normen för vektorer:
Där tr är matrisspåret och A * betecknar A:s hermiteska konjugat.
P-normen
En generalisering av Frobeniusnormen är p-normen:
Maximalnormen
Maximalnormen är det till beloppet största talet i matrisen:
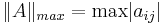 .
.