Lipschitzkontinuitet
Från Rilpedia
Lipschitzkontinuitet är ett villkor inom matematisk analys utvecklat av och namngett efter den tyske matematikern Rudolf Otto Sigismund Lipschitz. Grafiskt kan villkoret ses som ett ”mjukhetsvillkor” för funktioner, där funktionens lutning måste vara begränsad i alla punkter för att uppfylla villkoret.
Begreppet Lipschitz-kontinuitet ligger mellan begreppen kontinuitet och deriverbarhet. En deriverbar funktion är alltid Lipschitz-kontinuerlig, och en Lipschitz-kontinuerlig funktion är alltid kontinuerlig. Dock gäller inte omvändningen. En kontinuerlig funktion behöver inte vara Lipschitz-kontinuerlig, samtidigt som en Lipschitz-kontinuerlig funktion inte behöver vara deriverbar.
Innehåll |
Definitioner
Lipschitz-kontinuitet i en variabel
Funktionen 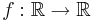 är Lipschitz-kontinuerlig på intervallet I omm det finns en lipschitz-konstant k > 0 sådan att för alla x och h, där
är Lipschitz-kontinuerlig på intervallet I omm det finns en lipschitz-konstant k > 0 sådan att för alla x och h, där 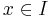 och
och 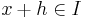 , gäller att
, gäller att 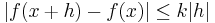 .
.
Lipschitz-kontinuitet i flera variabler
Funktionen 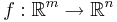 är Lipschitz-kontinuerlig på intervallet I omm det finns en lipschitz-konstant k > 0 för alla
är Lipschitz-kontinuerlig på intervallet I omm det finns en lipschitz-konstant k > 0 för alla 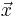 och
och 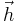 där
där 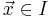 och
och 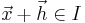 , gäller att
, gäller att 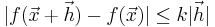
Lokal Lipschitz-kontinuitet
En funktion 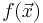 sägs vara lokalt Lipschitz-kontinuerlig i en punkt
sägs vara lokalt Lipschitz-kontinuerlig i en punkt 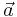 omm det finns någon omgivning kring punkten
omm det finns någon omgivning kring punkten 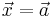 där funktionen
där funktionen 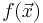 är Lipschitz-kontinuerlig.
är Lipschitz-kontinuerlig.
Egenskaper
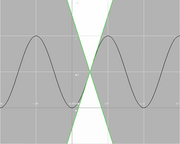
Att en funktion är Lipschitz-kontinuerlig betyder att dess lutning måste vara begränsad. För en variabel kan man grafiskt tänka sig att en Lipschitz-kontinuerlig funktion f kan inneslutas i två koner med axlarna längs x-axeln, vars toppar ligger i en gemensam punkt x på funktionen f (se bilden). Ifall det för varje punkt på f finns ett k, där k är lutningen på konernas sidor, så att f är helt innesluten av konen, så har vi en lokalt Lipschitz-kontinuerlig funktion. Om det dessutom finns ett och samma k för alla punkter på funktionen som gör att f alltid ligger inom konen, så kan vi säga att f är globalt Lipschitz-kontinuerlig.
Då en funktion har en Lipschitz-konstant 0 < k < 1 sägs funktionen vara en sammandragning.
Villkoret för Lipschitz-kontinuitet används i Picards sats, som nyttjas för att avgöra existensen för lösningar till differentialekvationer med begynnelsevärden.
Samband mellan kontinuitet, Lipschitz-kontinuitet samt deriverbarhet
Lipschitz-kontinuitet och deriverbarhet
- En funktion f som är deriverbar är också lokalt Lipschitz-kontinuerlig. Då derivatan av f är begränsad, så är f även globalt Lipschitz-kontinuerlig.
Enligt definitionen av riktningsderivata kan riktningsderivatan av funktionen 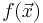 skrivas som
skrivas som
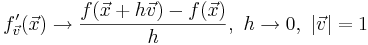
Omskrivning ger

Detta medför att f är lokalt Lipschitz-kontinuerlig för alla punkter på definitionsmängden, eftersom det finns en omgivning kring varje punkt x där
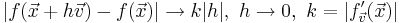
Detta innebär dock inte att f är globalt Lipschitz-kontinuerlig, eftersom 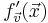 inte behöver vara obegränsad överallt även om den existerar. Ett exempel är funktionen
inte behöver vara obegränsad överallt även om den existerar. Ett exempel är funktionen 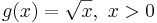 , vars derivata existerar på hela definitionsmängden och därför är lokalt Lipschitz-kontinuerlig överallt, men som däremot inte är globalt Lipschitz-kontinuerlig eftersom
, vars derivata existerar på hela definitionsmängden och därför är lokalt Lipschitz-kontinuerlig överallt, men som däremot inte är globalt Lipschitz-kontinuerlig eftersom 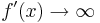 då
då 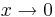 .
.
Men då 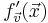 är begränsad på hela definitionsmängden kan man se att
är begränsad på hela definitionsmängden kan man se att
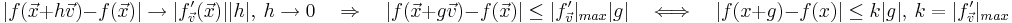
vilket är ekvivalent med att 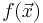 är globalt Lipschitz-kontinuerlig.
är globalt Lipschitz-kontinuerlig.
- Att en funktion är Lipschitz-kontinuerlig medför inte att den samtidigt är deriverbar.
Detta visas enklast genom ett exempel på en funktion som är Lipschitz-kontinuerlig men inte deriverbar. Ett sådant exempel är f(x) = | x | . I punkten x = 0 saknas derivata, men funktionen är fortfarande Lipschitz-kontinuerlig, eftersom funktionen är kontinuerlig och dess lutning är begränsad.
Lokal och global Lipschitz-kontinuitet
- En funktion som är globalt Lipschitz-kontinuerlig är även lokalt Lipschitz-kontinuerlig i alla punkter. Däremot gäller inte det omvända.
Detta samband kan utläsas direkt ur definitionerna. För en globalt Lipschitz-kontinuerlig funktion gäller att för alla punkter 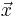 på funktionen så är lutningen till alla punkter
på funktionen så är lutningen till alla punkter 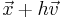 på funktionen begränsad. Därav följer även att det finns någon omgivning kring alla punkter
på funktionen begränsad. Därav följer även att det finns någon omgivning kring alla punkter 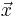 där lutningen mellan punkten x och alla punkter i den omgivningen är begränsad.
där lutningen mellan punkten x och alla punkter i den omgivningen är begränsad.
Funktionen f(x) = x2 är ett exempel på en funktion som är lokalt Lipschitz-kontinuerlig, men inte globalt. Kring varje enskild punkt x kan vi hitta en omgivning där lutningen är begränsad, vilket medför att f är lokalt Lipschitz-kontinuerlig för alla x. Däremot kommer lutningen att växa oändligt för stora positiva och negativa x. Därför finns ingen Lipschitz-konstant k så att 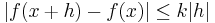 för alla x, och funktionen är därför inte globalt Lipschitz-kontinuerlig.
för alla x, och funktionen är därför inte globalt Lipschitz-kontinuerlig.
Kontinuitet och Lipschitz-kontinuitet
- Lipschitz-kontinuerliga funktioner är även kontinuerliga.
För en Lipschitz-kontinuerlig funktion f gäller enligt definitionen att
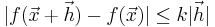
detta uttryck ska gälla för alla h och x där x och x + h ligger i definitionsmängden, vilket ger att det även gäller då h går mot 0.
Då h går mot 0 får vi direkt
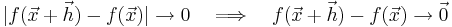
vilket är definitionen för kontinuitet.
- Att en funktion är kontinuerlig medför inte att den även är Lipschitz-kontinuerlig
Detta visas enklast genom att hitta en kontinuerlig funktion som inte är Lipschitz-kontinuerlig. Ett exempel på detta är 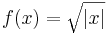 . Derivatan till denna funktion existerar i alla punkter utom x = 0. Däremot är
. Derivatan till denna funktion existerar i alla punkter utom x = 0. Däremot är 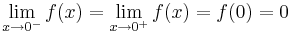 , vilket medför att f är kontinuerlig.
, vilket medför att f är kontinuerlig.
Då vi låter 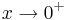 så kommer vi få att
så kommer vi få att 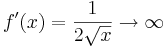 . Det saknas alltså en omgivning kring punkten x = 0 där vi har en begränsad lutning på funktionen f, vilket innebär att funktionen inte är lokalt Lipschitz-kontinuerlig, och därmed inte heller globalt Lipschitz-kontinuerlig.
. Det saknas alltså en omgivning kring punkten x = 0 där vi har en begränsad lutning på funktionen f, vilket innebär att funktionen inte är lokalt Lipschitz-kontinuerlig, och därmed inte heller globalt Lipschitz-kontinuerlig.
Källor
- PlanetMath.org - Lipschitz condition and differentiability
- University of Sussex - Spring 2006 Handout 3: Lipschitz condition and Lipschitz continuity
- Åbo Akademi - 8. Residykalkyl
- Michael Björklund, KTH - Existens och entydighet för ordinära differentialekvationer
- Analys i flera variabler, Arne Persson, Lars-Christer Böiers
- Matematisk Analys en variabel, Göran Forsling, Mats Neymark