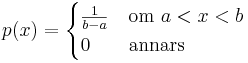Likformig sannolikhetsfördelning
Från Rilpedia
Likformig sannolikhetsfördelning innebär att sannolikheten är jämnt fördelad över utfallsrummet, dvs inget möjligt utfall är mer eller mindre sannolikt än något annat. Den likformiga sannolikhetsfördelningen antar antingen diskret eller kontinuerlig form.
Diskret likformig fördelning
Om man har N olika men lika sannolika utfall, x1, x2, ... ,xN, så är sannolikheten att inträffa för vart och ett av dessa utfall
- P(xk) = 1/N
Vid en dragning i Lotto (en process som får anses vara likformigt fördelad) är exempelvis sannolikheten att man först drar numret 6 precis 1/35. (N = 35 för Lotto eftersom det finns 35 olika nummer att välja mellan.)
Kontinuerlig likformig fördelning
En kontinuerlig likformig sannolikhetsfördelning kallas också rektangulärfördelning eftersom täthetsfunktionen får utseendet av en rektangel. Den har två parametrar, nedan kallade a och b, som betecknar den nedre respektive den övre gränsen för vilka värden den rektangulärfördelade slumpvariabeln kan anta. Täthetsfuktionen för rektangulärfördelningen är
och den kumulativa fördelningsfunktionen är