Kontinuitetsekvationen

Från Rilpedia

Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif

Kontinuitetsekvationen är en ekvation baserad på Reynolds transportteorem (RTT). Kontinuitetsekvationen säger att den netto utströmmade massan per tidsenhet är lika med minskningen av den inneslutna massan per tidsenhet.

Innehåll

Grundform

Den extensiva storheten B gäller då massa varför den intensiva storheten β blir 1 eftersom:

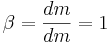
\beta={dm \over dm}=1

RTT blir då:

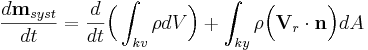{d \mathbf{m}_{syst} \over dt} = {d \over dt} \Big( \int_{kv}\rho dV \Big) +\int_{ky}\rho \Big( \mathbf{V}_r \cdot \mathbf{n} \Big) dA,

där kv står för kontrollvolym, ky för kontrollyta, ρ för densiteten, A för area, V för hastighet. 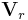\mathbf{V}_r är en relativ hastighetsvektor medan 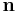\mathbf{n} är en enhetsvektor som är negativ för inflöde och positiv för utflöde. Dock är 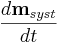{d \mathbf{m}_{syst} \over dt} lika med noll för en kontrollvolym.

Kontinuitetsekvationen är:

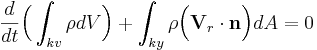
{d \over dt} \Big( \int_{kv} \rho dV \Big) + \int_{ky} \rho \Big( \mathbf{V}_r \cdot \mathbf{n} \Big) dA = 0

Kontinuitetsekvationen förenklas beroende på situation.

Fix kontrollvolym

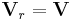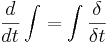\mathbf{V}_r=\mathbf{V} och {d \over dt} \int = \int {\delta \over \delta t}, dvs.

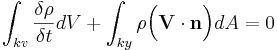
\int_{kv}{\delta\rho \over \delta t}dV + \int_{ky} \rho \Big( \mathbf{V} \cdot \mathbf{n} \Big) dA = 0

Endimensionell, stationär strömning i fix kontrollvolym

Vid stationär strömning är 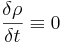{\delta\rho \over \delta t} \equiv 0

Vid endimensionell, stationär strömning i en fix kontrollvolym gäller då:

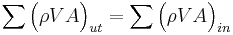\sum \Big( \rho V A \Big)_{ut} = \sum \Big( \rho V A \Big)_{in}, vilket ger att:

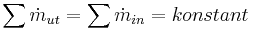
\sum \dot m_{ut} = \sum \dot m_{in}=konstant

Vid inkompressibelt flöde är densiteten konstant genom hela fluiden. Alltså gäller att 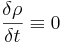{\delta\rho \over \delta t} \equiv 0.


Inkompressibelt flöde med fix kontrollvolym

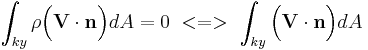
\int_{ky}\rho \Big(\mathbf{V} \cdot \mathbf{n}\Big) dA = 0 \ <=> \ \int_{ky} \Big(\mathbf{V} \cdot \mathbf{n}\Big) dA

Endimensionell, inkompressibel strömning genom kontrollvolym

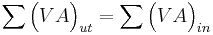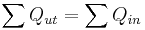\sum\Big( VA \Big)_{ut} = \sum \Big( VA \Big)_{in} dvs. \sum Q_{ut} = \sum Q_{in} och \sum \dot m_{ut} = \sum \dot m_{in}

Se även

Hämtad från "https://sv.rilpedia.org/wiki/Kontinuitetsekvationen"
Personliga verktyg