Gaussiska primtal

Från Rilpedia

Texten från svenska Wikipedia

Ett gaussiskt heltal z är ett gaussiskt primtal, om det endast har triviala faktoriseringar, alltså sådana där en av faktorerna är någon av "enheterna" 1, -1, den imaginära enheten i eller -i, men z självt inte är en enhet.

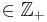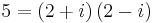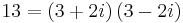Ett vanligt primtal p $\in \mathbb Z_+$ är också ett gaussiskt primtal, om och endast om antingen p = 2 eller p = 4n+3 för något naturligt tal n. Om däremot p = 4n+1, så har p en icketrivial faktorisering i ringen av gaussiska heltal. Exempelvis är $5 = (2+i)\, (2-i)$ och $13 = (3+2i)\, (3-2i)$ , så 5 och 13 är primtal i vanlig mening men inte gaussiska primtal.