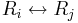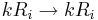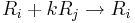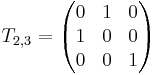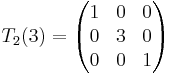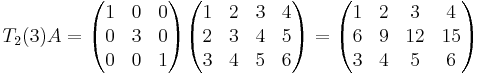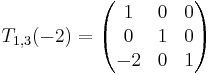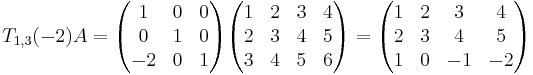Elementär matris
Från Rilpedia
Inom matematiken är elementära matriser matriser som skiljer sig från enhetsmatrisen på ett minimalt sätt. Matrismultiplikation med en elementär matris från vänster leder till en elementär radoperation i matrisen den elementära matrisen multipliceras med (multiplikation från höger leder till en elementär kolumnoperation).
Innehåll |
Ekvationssystemlösning
Elementära radoperationer ändrar inte lösningsmängden till ett linjärt ekvationssystem, något som används vid Gausselimination. Varje operation som man utför vid Gausselimination kan uttryckas som en elementär matris.
Radoperationer som elementära matriser
Det finns tre typer av elementära matriser som är sammankopplade med olika radbytesoperationer. Om vi kallar rad i i matrisen A för Ai (radvektor i), kan dessa uttryckas som:
- Radbyten, två rader byter plats:
- Radmultiplikation, en rad multipliceras med en konstant:
- Radaddition, en rad multiplicerad med en konstant läggs till en annan rad:
Radbytesmatriser
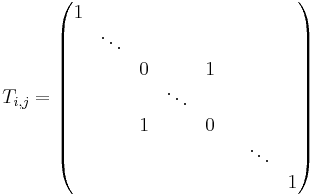
En elementär matris som byter två rader i och j i en matris:
Dvs, en matris med ettor i diagonalen förutom på två ställen, som markerar vilka rader som ska bytas. <math< T_{ij} fås enkelt genom att byta rad i med rad j i enhetsmatrisen.
Egenskaper
- Ti,j är sin egen invers,
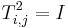 .
. - Determinanten för Ti,j är -1.
Exempel
Nedanstående matrisen byter plats på rad 1 och rad 2 i en matris av format 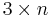 :
:
Multiplikation med en exempelmatris A:
Radmultiplikationsmatriser
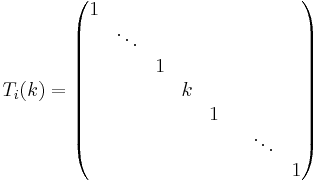
En elementär matris som multiplicerar en rad i med en konstant k kan uttryckas:
Egenskaper
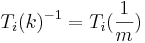 .
.- Matrisen är diagonal (enligt ovan är då även inversen diagonal).
- Determinanten är k.
Exempel
En matris som multiplicerar rad 2 i en matris med format 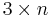 med talet 3 skulle uttryckas:
med talet 3 skulle uttryckas:
Multiplicerat med exempelmatrisen A:
Radadditonsmatriser
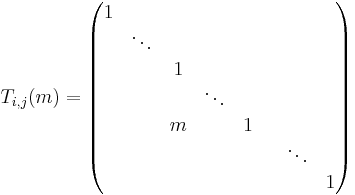
En matris som adderar en multipel m av en rad i till en annan rad j kan uttryckas:
Egenskaper
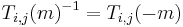
- Matrisen (och då även inversen) är triangulär.
- Determinanten för matrisen är 1.
Exempel
En matris som drar ifrån rad 1 multiplicerat med talet 2 från rad 3 i en matris med format 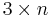 skulle uttryckas:
skulle uttryckas:
Multiplicerat med en exempelmatris A: