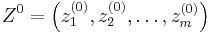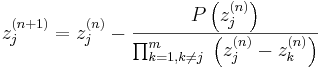Durand-Kerners metod

Från Rilpedia

Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif

Durand-Kerners metod är en numerisk metod för beräkning av nollställen till polynom. Den beskrevs 1960-1966 av E. Durand och I. Kerner men bygger på resultat av Karl Weierstrass och kallas därför ibland även Weierstrass metod eller W(D-K)-metoden.

Durand-Kerner går ut på att finna alla komplexa nollställen samtidigt. Givet ett moniskt polynom P(z) av grad m och en vektor av icke-reella begynnelsevärden

Z^0 = \left(z_1^{(0)}, z_2^{(0)}, \ldots, z_m^{(0)}\right)

består Durand-Kerner av iterationen

z_j^{(n+1)} = z_j^{(n)} - \frac{P\left(z_j^{(n)}\right)}{\prod_{k=1,k\neq j}^m \; \left(z_j^{(n)}-z_k^{(n)}\right)}

för j = 1, 2, ..., m. Z konvergerar då i praktiken nästan alltid mot polynomets samtliga nollställen, med kvadratisk konvergensordning om rötterna är enkelrötter. Varje iteration kräver O(m2) beräkningar.

Algoritmen kan härledas från Newtons metod.

Källor

Hämtad från "https://sv.rilpedia.org/wiki/Durand-Kerners_metod"
Personliga verktyg
På andra språk