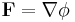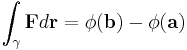Från Rilpedia

En skalärpotential är ett grundläggande begrepp inom vektoranalys och fysik (prefixet skalär används för att särskilja begreppet från det liknande begreppet vektorpotential, dock kallas skalärpotentialen ofta endast potential). Man säger att ett skalärfält φ är en potential till ett vektorfält 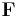om

där 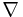är nablaoperatorn. I tillämpningar, som mekanik och elektromagnetism anges ofta funktionen − φ som potential istället.

Alla vektorfält har inte potentialer, de som har kallas konservativa fält eller potentialfält.

Kurvintegraler

Om vektorfältet 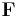är kontinuerligt deriverbar och har en potential φ i ett öppet område Ω, så är kurvintegralen över kurvan γ i Ω, som startar i 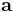och slutar i :

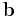med andra ord är kurvintegralen oberoende av vägen, om den har en potential.