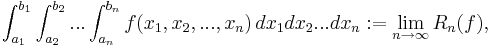Riemannintegration
Från Rilpedia
Riemannintegration, skapad av Bernhard Riemann, var den första rigorösa definitionen av integraler. Det finns flera andra definitioner, bland annat Lebesgueintegralen, som har teoretiska fördelar, men är mer komplicerade.
Formell definition
Riemanns idé var att definiera integralen för begränsade funktioner ![f : [a,b] \rightarrow \R](/w/images/sv.rilpedia.org/math/c/b/f/cbf6bcd3aa5cc7cdf73d8d1c12387715.png) med en "kolonn"approximation. Först delar man upp [a,b] i mindre intervall och sedan väljer man ut en punkt från varje intervall, då man får en kolonn med intervallets bred b − a och funktionen f:s värde i den utvalda punkten som höjd. En Riemannsumma är summan av de här kolonnernas area. De här Riemannsummorna approximerar arean under en funktionskurva och Riemannintegralen definieras så at den är ett gränsvärde av Riemannsummor.
med en "kolonn"approximation. Först delar man upp [a,b] i mindre intervall och sedan väljer man ut en punkt från varje intervall, då man får en kolonn med intervallets bred b − a och funktionen f:s värde i den utvalda punkten som höjd. En Riemannsumma är summan av de här kolonnernas area. De här Riemannsummorna approximerar arean under en funktionskurva och Riemannintegralen definieras så at den är ett gränsvärde av Riemannsummor.
Mer precist, partionera ![[a,b]\,](/w/images/sv.rilpedia.org/math/7/f/3/7f3408c72246eece3d5542fc853ce417.png) , så att ett antal mindre intervall bildas:
, så att ett antal mindre intervall bildas:
![\Delta_i = [c_{i-1}, c_i] \subset [a,b]\,](/w/images/sv.rilpedia.org/math/6/d/0/6d0288e4682d1f8728d72763e8d76dd6.png) ,
, 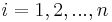 ,
,
och välj en punkt 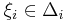 . Då definierar paret
. Då definierar paret
en kolonn vars area är
var 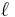 är längden av intervallet:
är längden av intervallet:
![\ell(\Delta_i)=\ell([c_{i-1}, c_i]) = c_i - c_{i-1}](/w/images/sv.rilpedia.org/math/1/a/5/1a5e8b076cf5041cebf7686bdb001517.png) .
.
En n-Riemannsumma för 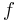 ,
, 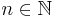 definieras som talet
definieras som talet
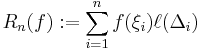 ,
,
dvs summan av alla kolonners areor. Riemannintegralen för funktionen 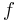 är talet
är talet
dvs bäst approximationen för arean under f:s funktionskurva.
Riemannintegralen i 
Riemann definierade endast Riemannintegralen i 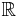 men metoden kan generaliseras till
men metoden kan generaliseras till  med samma kolonnapproximation. Låt
med samma kolonnapproximation. Låt
vara ett n-rätblock i  och
och 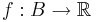 vara en begränsad funktion. Först partionerar man
vara en begränsad funktion. Först partionerar man 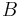 i n-rätblock
i n-rätblock
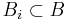 ,
, 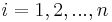 ,
,
och väljer 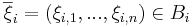 . Då paret
. Då paret
definierar en n-dimensionell kolonn vars mått är
där 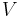 är n-dimensionella volymen för rätblocket:
är n-dimensionella volymen för rätblocket:
En n-Riemannsumma för 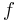 ,
, 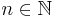 definieras som talet
definieras som talet
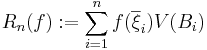 ,
,
dvs summan av alla kolonners storlek. Riemannintegralen för en funktion 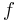 är talet
är talet
dvs bäst approximationen för (n+1)-dimensionella måttet under f:s funktionskurva.





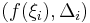
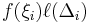
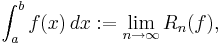
![B = [a_1,b_1]\times ... \times [a_n,b_n]](/w/images/sv.rilpedia.org/math/2/0/4/2048b9f989b20cda1dec99dde5261043.png)
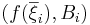
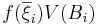
![V(B_i) = V([c_{i,1}, c_{i+1,1}] \times ... \times [c_{i,n}, c_{i+1,n}]) = \ell([c_{i,1}, c_{i+1,1}]) ... \ell([c_{i,n}, c_{i+1,n}]) = \prod_{k=1}^n (c_{i+1,k}-c_{i,k})](/w/images/sv.rilpedia.org/math/8/1/3/813a7c6a9d44e22fc00d6aaa0932ba8f.png)