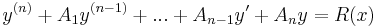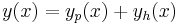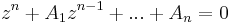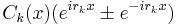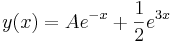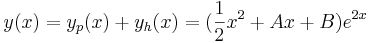Linjära ordinära differentialekvationer med konstanta koefficienter

Från Rilpedia

Hoppa till: navigering, sök

Texten från svenska Wikipedia

Linjära ordinära differentialekvationer med konstanta koefficienter är av formen

$y^{(n)} + A_{1}y^{(n-1)} + ... + A_{n-1}y' + A_{n}y = R(x) \,$

$y = y(x) \,$

Den allmänna lösningen till ekvationen är

$y(x) = y_{p}(x) + y_{h}(x) \,$

lösning = partikulärlösning + homogen lösning.

Homogena ekvationer

Differentialekvationen ovan sägs vara homogen när högerledet är 0. För att få den homogena lösningen till en ekvation vars högerled inte är 0, sätter man högerledet till 0.

Den första lösningsmetoden för ordinära differentialekvationer med konstanta koefficienter gavs av Euler.

Som ett exempel kan vi ta

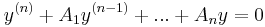$y^{(n)} + A_{1}y^{(n-1)} + ... + A_{n}y = 0 \,$ ,

där $A k$ är reella konstanter. Betrakta den algebraiska ekvationen

$z^{n} + A_{1}z^{n-1} + ... + A_n = 0 \,$

(byt ut $y (n)$ mot $z k$ , för alla k från 0 till n).
Om nu denna ekvation (kallad den karakteristiska ekvationen) har lösningarna $r 1,..., r m$ med multiplicitet : $p 1,..., p m$ respektive, så ges lösningen till differentialekvationen av

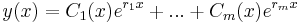$y(x)=C_1(x)e^{r_1x}+ ... + C_m(x)e^{ r_mx}$ ,

där $C k (x)$ är ett polynom av grad $p k - 1$ i x.

Det exakta utseendet av polynomen $C k$ kan bestämmas utifrån begynnelsevärden eller randvillkor.

Om lösningarna $r 1,..., r m$ till den karakterisitiska ekvationen inte är reella, så kommer lösningen innehålla termer på formen

$C_k(x)(e^{ir_kx}\pm e^{-ir_kx})$

vilket kan överföras på trigonometrisk form.

Partikulärlösningar

Partikulärlösningarna beror på hur högerledet i differentialekvationen ser ut, det vill säga vad $R (x)$ är.

Högerledet är ett polynom

Antag att högerledet är ett polynom av grad k. Knepet för att hitta partikulärlösningen går ut på att göra en ansättning, d.v.s. att man låter 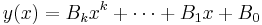$y(x)=B_k x^k+ \cdots +B_1 x+B_0$ , deriverar så många gånger som behövs, sätter in i ekvationen, och konstaterar att man får ett polynom på var sida likhetstecknet; och att två polynom är lika omm alla koefficienter stämmer överens.

Exempel

Antag att ekvationen är

y'' + 4 y = x 3 - 2 x + 1

.

Den homogena ekvationen $y'' + 4 y = 0$ har lösningarna $y h (x) = A cos(2 x) + B sin(2 x)$ , där A och B är två konstanter. För partikulärlösningen skriver vi

y p (x) = a x 3 + b x 2 + c x + d

Nu är a, b c och d konstanter som vi försöker bestämma. Andraderivatan, $y'' p (x)$ , blir då

y'' p (x) = 6 a x + 2 b

.

Insättning i ekvationen ger

6 a x + 2 b + 4 a x 3 + 4 b x 2 + 4 c x + 4 d = x 3 - 2 x + 1

Om polynomen till höger och till vänster ska vara lika, så måste:

4 a = 1

4 b = 0

6 a + 4 c = - 2

2 b + 4 d = 1

Detta linjära ekvationssystem har lösningen a=1/4, b=0, c=-7/8 och d=1/4. Alltså är partikulärlösningen

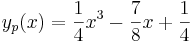
$y_p(x)= \frac{1}{4}x^3-\frac{7}{8}x+\frac{1}{4}$

och totala lösningen

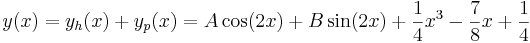
$y(x)= y_h(x)+y_p(x) = A\cos(2x)+B\sin(2x) + \frac{1}{4}x^3-\frac{7}{8}x+\frac{1}{4}$

Konstanterna A och B kan bestämmas ur randvillkor.

Högerledet är en exponentialfunktion

Om högerledet är en exponentialfunktion så måste man titta lite grand på den homogena lösningen innan man kan göra ansättningen. Om högerledet ges av $R (x) = e k x$ , och k är en lösning till den karakteristiska ekvationen, med multiplicitet p, så är det lämpligt att ansätta

y p (x) = a x p e k x

och sedan bestämma a. Om å andra sidan k inte är en lösning till den karakteristiska ekvationen, räcker det att ansätta y_p(x)=be^kx.

Exempel 1

Antag att vi vill lösa

y'(x) + y (x) = 2 e 3 x

Eftersom den homogena lösningen är

y h (x) = A e - x

så kan vi sätta y_p(x)=be^3x. Derivatan y′_p(x)=3be^3x, så om vi sätter in i ekvationen får vi:

y' p (x) + y p (x) = 3 b e 3 x + b e 3 x

Då ser vi att 4b=2, eller b=1/2 och att allmänna lösningen är

$y(x)=Ae^{-x}+\frac{1}{2}e^{3x}$

Exempel 2

Betrakta ekvationen

y''(x) - 4 y'(x) + 4 y = e 2 x

De homogena lösningarna är på formen

y h (x) = (A x + B) e 2 x

Den karakteristiska ekvationen har en dubbelrot, varvid partikulärlösningen bör ansättas som

y p (x) = a x 2 e 2 x

Efter deriveringar:

y' p (x) = a (2 x e 2 x + 2 x 2 e 2 x)

y'' p (x) = a (2 e 2 x + 8 x e 2 x + 4 x 2 e 2 x)

Insättning i ekvationen ger då att

y'' p (x) - 4 y' p (x) + 4 y p (x) = a (2 e 2 x + 8 x e 2 x + 4 x 2 e 2 x - 4(2 x e 2 x + 2 x 2 e 2 x) + 4 x 2 e 2 x) =

= a (2 + 8 x + 4 x 2 - 8 x - 8 x 2 + 4 x 2) e 2 x = 2 a e 2 x

För att högerled och vänsterled ska stämma överens, måste alltså a=1/2, och totala lösningen till ekvationen blir

$y(x)= y_p(x)+y_h(x)=(\frac{1}{2}x^2+Ax+B)e^{2x}$

där A och B bestäms ur randvillkor

Högerledet är en trigonometrisk funktion

Om högerledet är en trigonometrisk funktion med sinus- och/eller cosinus-termer antar man alltid att

$y p = a 1 cos b x + a 2 sin b x$

och löser som i tidigare exempel.
Observera att den antagna partikulärlösningen alltid ska ha både cosinus- och sinusterm, även om den ena termen saknas i differentialekvationen.

Högerledet är en diskontinuerlig funktion

Antag att högerledet f(x) är kontinuerligt i intervallen (a,b) och (b,c), samt att problemet är ett begynnelsevärdesproblem. Då löses ekvationen som vanligt i intervallet (a,b). (Där beter sig ekvationen precis som vanligt). Därefter beräknas lösningens värde, liksom så många derivator som behövs, då x=b. Dessa värden får sedan fungera som begynnelsevärden för den nya ekvationen som definieras på intervallet (b,c).

Om problemet är ett randvärdesproblem, ansätts konstanter för de begynnelsevärden som är okända. I princip räknar man sedan på samma sätt som ovan. Då kommer konstanterna följa med genom samtliga räkningar, och man kan avsluta med att jämföra värdet i den givna punkten på den lösning som räknats fram, med det värde som specificerats av randvillkoret.

Det är ofta enklare att använda Laplace-transformen för differentialekvationer där högerledet är en diskontinuerlig funktion.

Exempel

Låt y′′(x) + 4π² y(x) = f(x), där f(x) ges av 2-x då 0<=x<1, och x-2 då 1<=x<=2.

Antag även att vi har randvillkor y(0) = y(2) = 0

Den homogena lösningen i första intervallet (d.v.s. (0,1)) ges av

y_h(x)= A sin(2πx) + B cos(2πx).

För att få fram partikulärlösningen i det första intervallet ser vi på att den bör se ut som y_p = (2-x) / (4π²), en kontroll visar att det stämmer. Alltså har vi totala lösningen

y(x) = A sin (2πx) + Bcos(2πx) + (2-x) / (4π²).

Använder vi det begynnelsevillkor vi har, så får vi att

B + 2 / (4π²) = 0.

Därmed är

y(x) = A sin(2πx) - 2 / (4π²) cos(2πx) + (2-x) / (4π²),

så länge som x tillhör intervallet [0,1].

Nu gäller att få fram så mycket begynnelsevärden som möjligt till den andra delen av ekvationen: Insättning i den förra lösningen ger att

y(1) = -1 / (4π²)

(i just detta fall oberoende av A), och

y′(1) = 2πA - 1 / (4π²).

Den homogena lösningen i det andra intervallet skriver vi som

y_h = C sin(2πx) + D cos(2πx),

och partikulärlösningen är trevligt nog

y_p = (x - 2) / (4π²).

Totala lösningen alltså

y(x) = C sin(2πx) + D cos(2πx) + (x - 2) / (4π²).

Jämför med det begynnelsevärde vi känner, så fås y(1) = D - 1 / (4π²) = - 1 / (4π²), och y′(1) = 2πC + 1 / (4π²) = 2πA - 1 / (4π²).

Därmed är D = 0, och C = A - 1 / (4π³). Insättning i "dellösning 2" ger att

y(x) = (A - 1 / (4π³))sin(2πx) + (x - 2) / (4π²),

och det enda som borde återstå är att använda villkoret y(2) = 0 för att bestämma A. Dock ser vi att i just detta exempel så är y(2) = 0 oberoende av A. Kort sagt: vi har stött på ett fenomen som förekommer hos randvärdesproblem: det är inte säkert att en differentialekvation med randvillkor har en unik (entydig) lösning, det är till och med så att det inte ens är säkert att den har någon lösning över huvud taget. Betänk till exempel det ovanstående fallet där vi valt y(2) = 1 som ett av randvillkoren - den ekvationen är uppenbarligen inte möjlig att lösa.

För att sammanfatta exemplet:

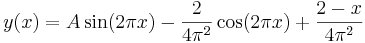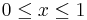
$y(x)=A \sin (2\pi x) - \frac{2}{4\pi^2} \cos(2\pi x) + \frac{2-x}{4\pi^2}$ då $0\leq x\leq 1$

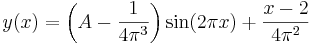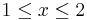
$y(x)=\left(A - \frac{1}{4\pi^3}\right) \sin (2\pi x) + \frac{x-2}{4\pi^2}$ då $1\leq x\leq 2$

Högerledet är en godtycklig funktion

Denna metod går ut på att ersätta konstanterna i den homogena lösningen med funktioner. Här visas metoden för differentialekvationer av andra ordningen. Då är den homogena lösningen av formen

$y h = C 1 y 1 (x) + C 2 y 2 (x)$

Man antar partikulärlösningen

$y p = v 1 (x) y 1 (x) + v 2 (x) y 2 (x)$

(I fortsättningen utlämnas (x) och högerledets funktion betecknas med H.)

Lösningen är

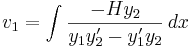
$v_{1} = \int_{}^{}{\frac {-Hy_{2}} {y_{1}y_{2}' - y_{1}'y_{2}}}\, dx$

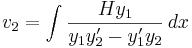
$v_{2} = \int_{}^{}{\frac {Hy_{1}} {y_{1}y_{2}' - y_{1}'y_{2}}}\, dx$

Integrering ger funktionerna $v 1$ och $v 2$ och integrationskonstanterna sätts till noll, eftersom endast en partikulärlösning behövs. Slutligen sätts $v 1$ och $v 2$ in i $y p$ och lösningen är färdig.

System av ekvationer

Ett system av lineära ODEer med konstanta koefficienter kan skrivas

x' = A x + b (t)

där $x$ är en vektorvärd funktion, $b$ en vektorvärd funktion och $A$ en konstant matris.

Den allmänna lösningen till detta system är summan av en partikulärlösning och den allmänna homogena lösningen, precis som ovan. Den allmänna homogena lösningen kan skrivas $e t A c$ där $e t A$ är matrisexponentialen och $c$ en godtycklig konstant vektor.

Eulers ekvation

Se även

Differentialekvation

Linjära ordinära differentialekvationer med konstanta koefficienter

Från Rilpedia

Innehåll

Homogena ekvationer

Partikulärlösningar

Högerledet är ett polynom

Exempel

Högerledet är en exponentialfunktion

Exempel 1

Exempel 2

Högerledet är en trigonometrisk funktion

Högerledet är en diskontinuerlig funktion

Exempel

Högerledet är en godtycklig funktion

System av ekvationer

Eulers ekvation

Se även

Visningar

Personliga verktyg

Sök

Navigering

Bibeln

Övrigt

Verktygslåda