Linjär diofantisk ekvation
Från Rilpedia
En linjär diofantisk ekvation är en diofantisk ekvation på formen a1x1 + a2x2 + ... + anxn = b där a1,...,an och b är konstanter, och x1,...,xn är variabler.
En linjär diofantisk ekvation i en variabel, ax = b, saknar lösningar om a inte delar b och har en lösning om a delar b nämligen x = b / a.
En linjär diofantisk ekvation i två variabler, ax + by = c (i), går att lösa om största gemensamma delaren (SGD) av a och b också delar c.
Innehåll |
Att lösa en linjär diofantisk ekvation i två variabler
Vi förutsätter här att SGD(a,b) = 1. Om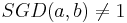 
delar vi först båda sidor av ekvationen med SGD(a,b) och får då en ny ekvation av samma sort och som har samma lösningar.
Steg ett
Hitta en lösning, (x0,y0), till hjälpekvationen ax + by = 1 (ii), vilket man enklast gör genom att använda euklides algoritm. Om, för att använda ett enkelt exempel, a = 25 och b = 4, ger euklides algoritm att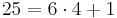 
vilket efter omskrivning blir 
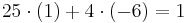, alltså är en lösning till hjälpekvationen (ii) i detta fallet x0 = 1 och y0 = − 6.
Steg två
Om hjälpekvationen (ii) multipliceras med c, ser man i acx0 + bcy0 = c att x = cx0 och y = cy0 är en lösning till (i), dock inte den enda.
Steg tre
Finn samtliga möjliga heltalslösningar. Betrakta ekvationen a(cx0 + nb) + b(cy0 − na) = c, där n är ett godtyckligt heltal. Eftersom anb − bna = 0 ser man att även denna likhet stämmer och därmed har vi funnit samtliga lösningar till (i), nämligen x = cx0 + nb och y = cy0 − na där n är ett godtyckligt heltal.
