Fas (matematik)
Från Rilpedia
- För andra betydelser, se fas.
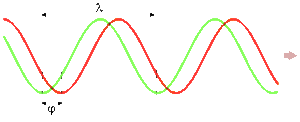
Fas är inom matematik och fysik ett uttryck som rör samtidigheten hos två vågor eller andra periodiska förlopp. Två likadana förlopp som varierar i takt så att de samverkar är i fas. Om de inte varierar i takt är de ur fas och fasskillnaden kan då anges som en fasförskjutning i form av en fasvinkel. Om de två förloppen varierar i takt men motverkar varandra är de i motfas.
Exempel: Två barn gungar intill varandra på var sin gunga. De gungar lika högt. Bara om de gungar i fas kan de hålla varandra i handen.
Innehåll[göm] |
Fasangivelse
Vanligen anges fasskillnaden i form av en fasvinkel. Vinkeln uttrycks ofta i grader när man talar om den, men i radianer vid matematiska beräkningar. En hel period motsvarar 360˚. En fasskillnad på 10% av en hel period är alltså 36˚. Kopplingen mellan grad av samtidighet och vinkel är mest uppenbar när man betraktar roterande hjul eller sinusformade vågor.
Exempel: En vevstake på ett ånglok överför kolvens fram- och återgående rörelse till rotationsrörelse vid hjulen. Loket har svårt att komma igång om vevstaken är i sitt bakre eller främre läge. Den bör helst vara nära sitt övre eller nedre läge för att rörelsen ska kunna påbörjas och säkert gå åt rätt håll. Därför är vevstaken på högerhjulen fasförskjuten 90˚ mot vevstaken på vänsterhjulen. När den är i ett dåligt läge på ena sidan, är den i ett bra läge på andra, och loket kan alltid starta.
Matematiskt kan man beskriva två vågor a(t) och b(t) med olika fas som:
- a(t) = sin(ωt)
- b(t) = sin(ωt + Φ)
Här är ω vinkelhastigheten, ett mått på vågens frekvens, och ωt blir en vinkel som ständigt ökar med tiden t och får sin(ωt) att öka och minska sitt värde som en våg. Den konstanta fasvinkeln mellan vågorna är Φ.
Fasskillnaden kan också anges som en tidsskillnad mellan de två periodiska förloppen. Men om frekvensen på rotationen eller vågrörelsen ändras, kommer samma fasskillnad att ge upphov till en annan tidsskillnad. Vevstakarnas rörelser på ett ånglok har konstant fasvinkel men en tidsskillnad som beror på hur fort loket rullar.
Fas är relativ
För ett isolerat förlopp är begreppet fas helt irrelevant. Fas får bara mening vid jämförelse med ett annat förlopp som kan användas som norm. Oftast jämför man två skilda men samtidiga förlopp, men det går också att jämföra ett förlopp som genomgått en förändring med hur det hade varit utan denna förändring.
Den som beskriver en svängning med formeln
- s(t) = sin(ωt + Φ)
antyder att det finns en norm som är sin(ωt) och att den beskrivna svängningen avviker med fasvinkeln Φ från denna norm.
Fas mellan olikartade förlopp
Enklast är att bestämma fasen mellan likartade förlopp. Jämför exempelvis svängningen cos(ωt) med sin(ωt). De har exakt samma form. Enda skillnaden är att sin(ωt) hela tiden når sina värden 90˚ efter cos(ωt), vilket alltså är fasvinkeln mellan dem. Därför kan vi också skriva sin(ωt) som cos(ωt – 90˚).
Om de två förloppen har något olika frekvens, uppstår en fasvinkel som hela tiden ökar. Ett exempel är två kyrkklockor som ringer. De kan slå första slaget samtidigt, men vid nästa slag kommer den lilla klockan något före. För varje slag kommer klockorna alltmer ur fas. Så småningom "varvar" lilla klockan den stora. Då har fasskillnaden blivit 360˚ och slagen ligger åter i fas. Vid den typ av modulation som kallas fasmodulering måste man tillfälligt ändra bärvågens frekvens något för att uppnå ett annat fasläge än man hade innan.
Om förloppen är av olika typ, är det inte självklart hur fasläget mellan dem ska mätas. Ett barn kan gunga på en gunga och ömsom sträcka fram, ömsom dra tillbaka fötterna för att inte tappa farten. Gungandet och benrörelserna ha samma frekvens. Fasläget mellan rörelserna kan dock inte anges förrän man definierar vad som ska anses vara "början" på var och en av dem. Likaså kan man tvista om hur en EKG-våg och en sinusvåg av samma frekvens ska vara för att anses ligga i fas.
Utifrån ett givet förlopp kan man alltid skapa ett förlopp som går i motfas genom att byta tecken på momentanvärdet. Svängningen –sin(ωt) går i motfas till +sin(ωt), och summerar vi dem så tar de ut varandra. Men det är bara för förlopp med en speciell typ av symmetri som man även kan åstadkomma motfas genom fasförskjutning med en halv period. Det fungerar för sinusvågor, där sin(ωt + 180˚) går i motfas till sin(ωt), men det gäller inte för förlopp i allmänhet. Antag att vi har korta, åtskilda ljudpulser med 1 sek mellanrum, exempelvis tickljudet från en klocka. Om vi lägger till ett likadant tickljud som är en halv sekund fördröjt, tar ljuden inte ut varandra. I stället får vi dubbelt så många tickljud.
Övrigt
I en hantlangarkedja kan man inte samverka om alla vänder sig åt samma håll samtidigt. Man måste parvis vända sig mot varandra för att överlämna godset till nästa person. Samarbetsmässigt arbetar man alltså i fas (i samverkan) när man matematiskt sett rör sig ur fas, närmare bestämt i motfas.
I trefassystemet distribueras elektrisk energi med växelström i tre olika faslägen, 0˚, 120˚ och 240˚. För detta används tre separata ledningar som i ordning kallas L1, L2 och L3 och som ofta benämns "faser". Om man har tillgång till två av ledningarna kan man mäta upp fasskillnaden mellan dem. Den är 120˚ oberoende av vilka två "faser" man fått. Man kan även avgöra vilken fas som ligger före. Eftersom fas är ett relativt begrepp, räcker dock inte detta för att man entydigt ska kunna identifiera ledningarna som L1, L2 eller L3. Då måste man ha tillgång till en ledning med känd märkning.