Carlesonmått
Från Rilpedia
Carlesonmått är ett mått som är av betydelse i harmonisk analys. Carlesonmåttet är uppkallat efter Lennart Carleson.
Innehåll |
Definition
Carlesonmåttet är ett mått som kan mäta volymen för en domäns rand i  .
.
Mer precist, låt  vara en öppen mängd vars rand
vara en öppen mängd vars rand  . Ett Borelmått
. Ett Borelmått 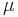 till
till 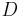 är ett Carlesonmått om det finns
är ett Carlesonmått om det finns 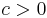 så att för alla
så att för alla 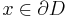 och
och 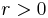
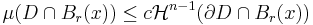 ,
,
där 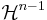 är det n-1-dimensionella Hausdorffmåttet och Br(x) är bollen med mittpunkt x och radie r.
är det n-1-dimensionella Hausdorffmåttet och Br(x) är bollen med mittpunkt x och radie r.
Ett n-1-dimensionellt Hausdorffmått är det mest naturliga måttet här eftersom det i  mäter randens yta.
mäter randens yta.
Historia
Carleson definierade Carlesonmåttet så att han kunde bevisa den kända Koronasatsen som behandlar funktioner nära till randen.
Se även
Referenser
- Lennart Carleson, Interpolations by bounded analytic functions and the corona problem (1962) Ann. of Math. 76. sid. 547-559. ISSN: 0003-486X.



