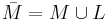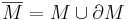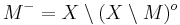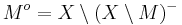Slutet hölje
Från Rilpedia
Det slutna höljet till en mängd M är inom matematik är mängden av alla punkter som, intuitivt uttryckt, ligger "nära" M.
Innehåll |
Definition
Låt M vara en mängd och låt L vara mängden av alla M:s hopningspunkter. Då definieras det slutna höljet av M som unionen av M och L:
Detta kan även uttryckas som att slutna höljet till M är M med sin rand:
Egenskaper
Det slutna höljet har följande egenskaper:
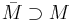 .
.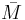 är den minsta slutna mängden som innehåller M.
är den minsta slutna mängden som innehåller M.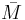 är snittet av alla slutna mängder som innehåller hela M.
är snittet av alla slutna mängder som innehåller hela M.- M är sluten om och endast om
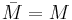 .
. - Om
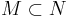 så följer att
så följer att 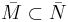 .
.
Ibland används den andra eller den tredje egenskapen som definitionen av det slutna höljet.
Exempel
- I alla rum X så är det slutna höljet av den tomma mängden den tomma mängden och
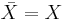 .
. - Det slutna höljet till det öppna intervallet ]0,1[ är det slutna intervallet [0,1].
- Det slutna höljet till de rationella talen är de reella talen, man säger att de rationella talen är en tät delmängd till de reella talen.
- I komplexa talplanet är det slutna höljet av
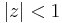 (den öppna skivan) lika med
(den öppna skivan) lika med 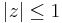 (den slutna skivan).
(den slutna skivan).
Slutet hölje som operator
I ett rum X, låt M vara en mängd, M − det slutna höljet till M och Mo det inre till M. Följande samband kopplar ihop det slutna höljet med det inre:
Där 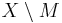 är komplementet till M i X.
är komplementet till M i X.