Från Rilpedia

Argumentprincipen är ett resultat inom komplex analys som uttrycker en analytisk funktions uppförande i ett givet område givet uppförandet på områdets rand.

Formulering

Låt f vara analytisk och nollskild på och innanför den slutna kurvan γ, med undantag för ändligt många punkter, alla innanför γ, där alla eventuella singulariteter är poler. Då gäller 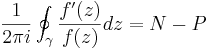, där N och P är antalet nollställen respektive poler, inräknat multiplicitet.

• Man kan visa att 2π(N − P) är argumentvariationen av f(z) då z genomlöper kurvan γ.
• Då tillämpar argumentprincipen på polynom, som saknar poler och kan faktoriseras givet dess nollställen, visar sig argumentprincipen ge uttryck för följande intuitiva sanning:

Om man mäter vinkeln från en viss punkt P till en punkt genomlöpande randen till ett givet område, så ökar vinkeln med 2π omm punkten ligger i området, med 0 omm punkten ligger utanför. Notera att argumentet av noll ej är definierat, så att argumentvariationen ej är definierad då punkten ligger i områdets rand.

Se även

• Rouchés sats