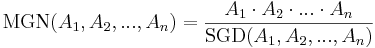Minsta gemensamma nämnare

Från Rilpedia

Texten från svenska Wikipedia

Minsta gemensamma nämnare, förkortat MGN, är ett heltal som används när man ska förenkla summan av rationella tal (tal skrivna som bråk) eller polynom skrivna som bråk. Talet används för att reducera bråkuttrycken, men det är också användbart för att lösa kostnadskalkyler med objekt av olika ekonomisk livslängd inom företagsekonomi. Den engelska termen för MGN är Least common denominator, LCD.

MGN är den minsta multipeln av bråkuttryckens nämnare. D.v.s. om nämnarna är heltalen A₁, A₂,...,A_n så är MGN minsta möjliga tal X sådant att X = k_iA_i, där k_i är heltal.

MGN kan beräknas med hjälp av största gemensamma delaren av nämnarna. Om största gemensamma delaren av A₁, A₂, ...,A_n betecknas med SGD(A₁, A₂, ...,A_n) så ges minsta gemensamma nämnaren av uttrycket

För specialfallet n = 2 reduceras uttrycket till

.

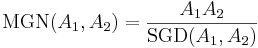Exempel

Vad blir MGN för 7÷792 + 3÷616. Om största gemensamma delaren för 792 och 616 beräknas genom

792 = 1·616 + 176

616 = 3·176 + 88

176 = 2·88

är alltså SGD(792, 616) = 88. Detta ger MGN(792, 616) =792·616/88 = 5 544. Med hjälp av 616 = 7·88 och 792 = 9·88 kan uttrycket förenklas till

7÷792 + 3÷616 = (7·7 + 3·9)/5 544 = 76÷5 544.

Notera: Om problemet hade varit 'förenkla 616÷792' hade det räckt med att beräkna SGD.

Se även

• Minsta gemensamma multipel
• Största gemensamma delare