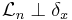Singulärt mått
Från Rilpedia
Version från den 5 april 2009 kl. 09.39 av Zorrobot (Diskussion)
Ett singulärt mått är ett begrepp inom matematisk måtteori. Måttet är singulärt med andra måttet om där finns en mängd som är nollmängd och vars komplement är nollmängd med avseende på andra måttet.
Innehåll |
Formell definition
Låt 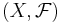 vara ett mätbart rummet och
vara ett mätbart rummet och ![\mu : \mathcal{F} \rightarrow [0,\infty]\,](/w/images/sv.rilpedia.org/math/a/e/6/ae6f627ce2b2a61aa53a4fd65310ceeb.png) och
och ![\nu : \mathcal{F} \rightarrow [0,\infty]\,](/w/images/sv.rilpedia.org/math/5/4/e/54ed7ea26ca6d38b75da8770edeef617.png) mått.
mått.
Måttet 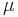 är singulärt med avseende på måttet
är singulärt med avseende på måttet 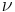 om där finns
om där finns 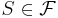 så att
så att
 ,
,
dvs S är 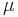 -nollmängden och X\S är
-nollmängden och X\S är 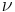 -nollmängden.
-nollmängden.
Om 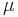 är singulärt
är singulärt 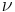 man betäckar
man betäckar
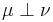 .
.
Operatoren 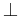 kommutativ:
kommutativ:
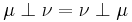 .
.
Exempel
Lebesguemåttet är singulärt med avseende på Diracmåttet. Låt 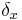 vara Diracmåttet i punkten
vara Diracmåttet i punkten 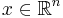 . Eftersom
. Eftersom 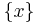 är sluten mängden, det är Borelmängden och därför Lebesguemätbara mängden. Å andra sidan
är sluten mängden, det är Borelmängden och därför Lebesguemätbara mängden. Å andra sidan
 ,
,
dvs {x} är 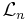 -nollmängden och Rn\{x} är
-nollmängden och Rn\{x} är 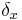 -nollmängden. Så att
-nollmängden. Så att
för alla 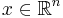 .
.
Tillämpningar
- Man kan fördela alla sigma-ändligt mått till singulära och absolut kontinuerliga bitar med Lebesgues uppdelningsatsen.