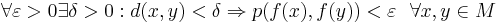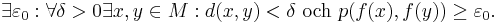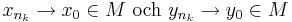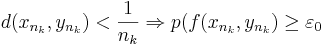Heine-Cantors sats

Version från den 24 januari 2009 kl. 06.41 av Zorrobot (Diskussion)

(skillnad) ← Äldre version | Nuvarande version (skillnad) | Nyare version → (skillnad)

Texten från svenska Wikipedia

Heine-Cantors sats är en matematisk sats uppkallad efter Georg Cantor och Eduard Heine som säger att om M är ett kompakt metriskt rum så är varje kontinuerlig funktion 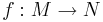$f:M \to N$ , där N är ett metriskt rum, likformigt kontinuerlig.

Bevis

Låt 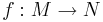$f:M \to N$ vara en funktion från M med metrik d till N med metrik p. Att f skulle vara likformigt kontinuerlig innebär

$\forall \varepsilon > 0 \exists \delta>0: d(x,y) < \delta \Rightarrow p(f(x), f(y)) < \varepsilon ~~ \forall x,y \in M$

antag nu att f inte är likformigt kontinuerlig, dvs:

$\exists \varepsilon_0: \forall \delta > 0 \exists x,y \in M: d(x,y) < \delta ~ \mathrm{och} ~ p(f(x), f(y)) \geq \varepsilon_0.$

Välj två följder, $x n$ och $y n$ så att:

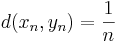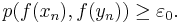
$d(x_n, y_n) = \frac{1}{n}$ och $p(f(x_n), f(y_n)) \geq \varepsilon_0.$

Då M är kompakt existerar det (Bolzano-Weierstrass sats) två delföljder som konvergerar

$x_{n_k} \to x_0 \in M ~ \mathrm{och} ~ y_{n_k} \to y_0 \in M$

så det följer att:

$d(x_{n_k}, y_{n_k}) < \frac{1}{n_k} \Rightarrow p(f(x_{n_k}, y_{n_k}) \geq \varepsilon_0$

den första delen ger att $x 0 = y 0$ och den andra säger att 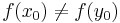$f(x_0) \neq f(y_0)$ , vilket uppenbarligen är en motsägelse.