Aperiodisk graf
Från Rilpedia
Version från den 23 mars 2009 kl. 19.37 av Calle (Diskussion)
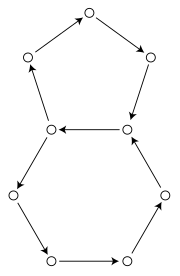
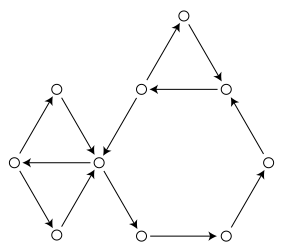
Inom det matematiska området grafteori är en aperiodisk graf en riktad graf där det inte finns något heltal k som delar längderna av alla cykler. Ekvivalent kan man säga att en aperiodisk grafs cykellängder har minsta gemensamma nämnaren 1 (denna minsta gemensamma nämnaren brukar kallas grafens period).
Grafer som inte kan vara aperiodiska
I varje riktad bipartit graf har alla cykler en längd som är delbar med två och därför kan riktade bipartita grafer inte vara aperiodiska. I varje riktad graf utan cykler delar alla tal alla cykellängder (eftersom det inte finns några cykler), så riktade grafer utan cykler kan inte vara aperiodiska. I varje riktad cyklisk graf finns endast en cykel, så en sådan graf har en period som är lika med cykellängden och därmed ej aperiodisk.