Bipartit graf
Från Rilpedia
En bipartit graf är en graf vars hörnmängd V(G) kan partitioneras som 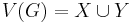 där
där 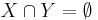 och där varje kant
och där varje kant 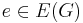 kan skrivas på formen e = {x,y}, där
kan skrivas på formen e = {x,y}, där 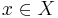 och
och 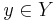 . I så fall säges G ha bipartitionen (X,Y). Detta kan även uttryckas så att noderna i en bipartit graf kan indelas i två mängder, sådana att inga kanter går mellan två noder i samma mängd.
. I så fall säges G ha bipartitionen (X,Y). Detta kan även uttryckas så att noderna i en bipartit graf kan indelas i två mängder, sådana att inga kanter går mellan två noder i samma mängd.
Innehåll |
Egenskaper
- En graf är bipartit om och endast om den inte har några cykler av udda längd.
- För bipartita grafer med icke-tomma kantmängder gäller att χ = 2, där χ är det kromatiska talet.
- Varje bipartit graf är en perfekt graf.
Exempel
Varje graf som inte har någon cykel av udda längd är bipartit. Exempel på grafer som uppfyller detta är träd och cykliska grafer med ett jämnt antal bågar.
Tillämpningar
Bipartita grafer har tillämpningar till områden utanför matematiken, till exempel inom schemaläggning.
Generalisering
En k-partit graf är en graf vars hörnmängd kan partitioneras som 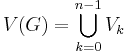 , och där varje kant
, och där varje kant 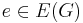 kan skrivas på formen e = {x,y}, där
kan skrivas på formen e = {x,y}, där 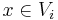 och
och 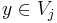 och
och 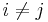 . En graf har kromatiskt tal k, om och endast om den är ,,k..-partit men inte (k-1)-partit.
. En graf har kromatiskt tal k, om och endast om den är ,,k..-partit men inte (k-1)-partit.




