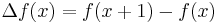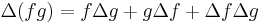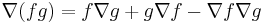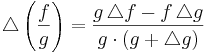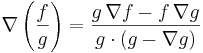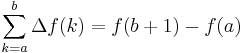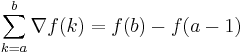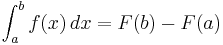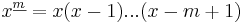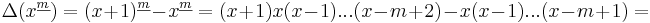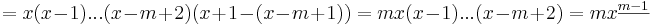Differensoperator
Från Rilpedia
Inom matematiken är en differensoperator en operator som avbildar en funktion f(x) till en annan funktion f(x + a) − f(x + b).
De två enklaste differensoperatorerna är framåtdifferensoperatorn:
och bakåtdifferensoperatorn:
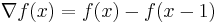 .
.
Framåtdifferensoperatorn spelar inom diskret matematik en liknande som derivatan spelar inom kontinuerlig matematik. Differensekvationer kan med differensoperatorn ofta lösas på ett liknande sätt som differentialekvationer löses med differentialoperatorn.
Räkneregler
För både  och
och 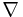 gäller att:
gäller att:
- Om c är konstant är:
- Δc = 0
- Linjäritet, för funktioner f,g och konstanter a,b:
Följande regler är olika för  och
och 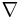 :
:
- Produktregel:
- Kvotregel:
- Summering:
Detta göra att summeringar av funktioner f där man vet att Δg = f blir väldigt enkla. Likheter kan ses med integraler, om F(x) är en primitiv funktion fill f(x):
Exempel
En fallande potens av ett tal x är ett tal sådant att:
Fallande potenser har väldigt enkla differenser:
Dvs, kort uttryckt:
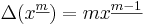 .
.