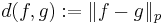Pseudometriskt rum
Från Rilpedia
I matematiken är ett pseudometriskt rum en mängd med en tilldelad avståndsfunktion, en pseudometrik, i likhet med ett metriskt rum, men i ett pseudometriskt rum kan avståndsfunktionen bli noll även om elementen inte är lika.
Ibland, framförallt inom funktionalanalys, används termen semimetrisk rum om pseudometriska rum, doch har semimetriskt rum en annan betydelse inom topologi.
Innehåll |
Definition
Ett pseudometriskt rum är ett par (X,d) där X är en mängd och d är en pseudometrik. Villkoren för en pseudometrik är, för 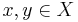 :
:
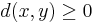
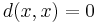
 (symmetri)
(symmetri)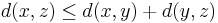 (triangelolikhet)
(triangelolikhet)
Skillnaden mellan en metrik och en pseudometrik är alltså att för en pseudometrik implicerar inte d(x,y) = 0 att x = y, vilket är falllet för en vanlig metrik.
Exempel
Pseudometriska rum dyker upp i funktionalanalys. Om man t.ex. betraktar ett rum X och utifrån detta skapar ett nytt rum 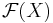 som består av alla funktioner
som består av alla funktioner 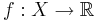 . Om vi väljer ett speciellt element
. Om vi väljer ett speciellt element 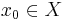 , kan vi få en pseudometrik på
, kan vi få en pseudometrik på 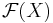 genom:
genom:
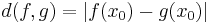 .
.
där 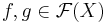 .
.
I ett vektorrum kan man inducera en pseudometrik från en pseudonorm, p genom:
Metriska rum från pseudometriska rum
Man kan, utgående från ett pseudometriskt rum, bilda ett metriskt rum.
Låt (X,d) vara ett pseudometriskt rum. Definiera en ekvivalensrelation, ˜, på X genom:
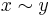 om
om 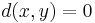
och låt X * vara mängden av ekvivalensklasser som uppstår. Definiera sedan metriken:
då (X * ,d * ) är ett metriskt rum.
Exempel
Det viktiga exempel för den här ekvivalensrelation är Lp-rummet när Lp-normen
för 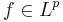 formar en pseudometrik
formar en pseudometrik
för 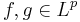 . Vi definiera Lp-rummet (med samma symbol) så att det har metriken
. Vi definiera Lp-rummet (med samma symbol) så att det har metriken 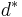 för ekvivalensklasser.
för ekvivalensklasser.




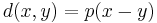
![d^*([x],[y]) = d(x,y)\,](/w/images/sv.rilpedia.org/math/8/0/e/80e9d28a65a8993963d3d98c27af4ae8.png)