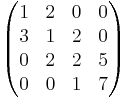Tridiagonal matris

Från Rilpedia

Version från den 22 oktober 2008 kl. 17.58 av Alexbot (Diskussion)
(skillnad) ← Äldre version | Nuvarande version (skillnad) | Nyare version → (skillnad)
Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif

En tridiagonal matris är inom matematiken en matris som är "nästan" diagonal, mer specifikt har den nollskilda element endast i huvuddiagonalen samt diagonalerna precis under och över huvuddiagonalen.

Ett exempel på en tridiagonal matris:

\begin{pmatrix} 1 & 2 & 0 & 0 \\ 3 & 1 & 2 & 0 \\ 0 & 2 & 2 & 5 \\ 0 & 0 & 1 & 7 \end{pmatrix}

Egenskaper

Tridiagonala matriser är ett specialfall av Hessenbergmatriser.

Om elementen i en tridiagonal matris A är symmetriska med avseende på tecknet, dvs ak,k + 1ak + 1,k > 0, så kan den via basbyte omvandlas till en hermitesk matris.

Många algoritmer inom linjär algebra är betydligt snabbare när de appliceras på diagonala matriser, något som ofta även gäller för tridiagonala matriser.

Hämtad från "https://sv.rilpedia.org/wiki/Tridiagonal_matris"
Personliga verktyg