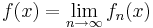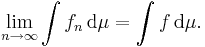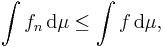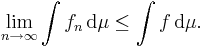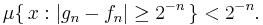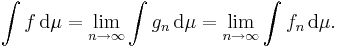Monotona konvergenssatsen

Från Rilpedia

Version från den 16 januari 2009 kl. 04.09 av Calle (Diskussion)
(skillnad) ← Äldre version | Nuvarande version (skillnad) | Nyare version → (skillnad)
Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif

Monotona konvergenssatsen är ett teorem inom den matematiska analysen som förkunnar att om μ är ett mått på en mängd X och fn är en växande följd av funktioner som antar icke negativa värden och är integrerbara med avseende på μ, så uppfyller funktionen

f(x) = \lim_{n \rightarrow \infty} f_n(x)

likheten

\lim_{n \rightarrow \infty} \int f_n \, \mathrm{d}\mu = \int f \, \mathrm{d}\mu.

Bevis

Olikheten 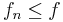f_n \leq f ger att

\int f_n \, \mathrm{d} \mu \leq \int f \, \mathrm{d}\mu,

med en naturlig tolkning i det fall att f inte är integrerbar. Det följer att

\lim_{n\to \infty} \int f_n \, \mathrm{d} \mu \leq \int f \, \mathrm{d}\mu.

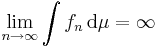Om \lim_{n\to \infty} \int f_n \, \mathrm{d} \mu = \infty , så är utsagan i satsen uppenbarligen sann. Antag att 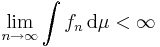\lim_{n\to \infty} \int f_n \, \mathrm{d} \mu < \infty . Då gäller att

\int |f_m - f_n| \, \mathrm{d}\mu = \int f_m\, \mathrm{d}\mu - \int f_n \, \mathrm{d} \mu \to 0, \quad m \geq n \to \infty .

Tag enkla funktioner gn sådana att 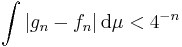\int |g_n - f_n| \, \mathrm{d} \mu < 4^{-n} . Då är

\mu \{\, x: |g_n - f_n| \geq 2^{-n} \, \} < 2^{-n}.

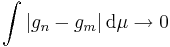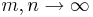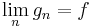Det följer att \int |g_n - g_m| \, \mathrm{d}\mu \to 0 när m,n \to \infty, och \lim_n g_n = f nästan överallt. Sålunda är f integrerbar och

\int f \,\mathrm{d} \mu = \lim_{n\to \infty} \int g_n \,\mathrm{d} \mu = \lim_{n \to \infty} \int f_n \,\mathrm{d} \mu.
Hämtad från "https://sv.rilpedia.org/wiki/Monotona_konvergenssatsen"
Personliga verktyg