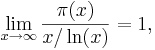Primtalssatsen
Från Rilpedia
Version från den 29 maj 2009 kl. 23.43 av Xqbot (Diskussion)
Primtalssatsen är ett talteoretiskt resultat som ger en uppskattning av hur tätt primtalen ligger. Om vi betecknar antalet primtal som är mindre än eller lika med x med π(x) säger satsen att
dvs att π(x) är ungefär lika med x/ln(x) för stora x.
Resultatet uppställdes som en förmodan av Adrien-Marie Legendre 1798, men bevisades först 1896 av Jacques Hadamard och Charles de la Vallée Poussin (oberoende av varandra).