Laurentserie
Från Rilpedia
Version från den 17 maj 2009 kl. 05.11 av ArthurBot (Diskussion)
En Laurentserie är en serie på formen 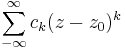 , där
, där 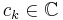 . En Laurentserie konvergerar i områden av formen r < | z | < R. Detta kan inses genom att betrakta de två serierna
. En Laurentserie konvergerar i områden av formen r < | z | < R. Detta kan inses genom att betrakta de två serierna
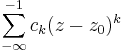 , som konvergerar på ett område av formen r < | z | och
, som konvergerar på ett område av formen r < | z | och 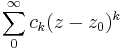 , som konvergerar på ett område av formen | z | < R. Koefficienterna ck för Laurentserieutvecklingen av en funktion f, analytisk i ett område av typen r < | z | < R, kan bestämmas ur Cauchys integralformel:
, som konvergerar på ett område av formen | z | < R. Koefficienterna ck för Laurentserieutvecklingen av en funktion f, analytisk i ett område av typen r < | z | < R, kan bestämmas ur Cauchys integralformel:
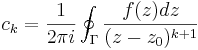 , där Γ är en positivt orienterad kurva med
, där Γ är en positivt orienterad kurva med 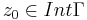 , på vilken f är analytisk.
, på vilken f är analytisk.
Om f i själva verket är analytisk i området | z | < R, visar Cauchys integralsats, som säger att kurvintegralen av en funktion som är analytisk innanför integrationskonturen är noll, att Laurentserieutvecklingen är en Taylorserie.



