Hel funktion

Från Rilpedia

Texten från svenska Wikipedia

En matematisk funktion sägs vara hel om den är analytisk i hela det komplexa talplanet. Alla polynom, samt även f(z) = sin(z), f(z) = cos(z) och f(z) = a^z för alla 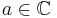är exempel på hela funktioner. Funktionerna 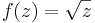, f(z) = | z | och 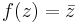(det komplexa konjugatet av z) är exempel på funktioner som är kontinuerliga men ej hela.

Utifrån definitionen av hel funktion kan man bevisa att varje hel funktion också har en hel derivata, därför är alla hela funktioner oändligt deriverbara.

Varje hel funktion kan uttryckas som en potensserie som är konvergent i hela det komplexa talplanet.