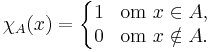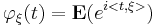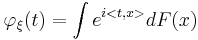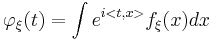Karakteristisk funktion
Från Rilpedia
Inom matematiken kan namnet karakteristisk funktion referera till olika saker. Framförallt förekommer två olika betydelser, av vilka den första förekommer i ett antal olika discipliner av matematik, medan den andra förekommer inom sannolikhetsteori och matematisk statistik. Ibland kan namnet även referera till det karakteristiska polynomet inom linjär algebra.
Definition (vanlig betydelse)
Låt X vara en godtycklig mängd, och 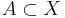 en delmängd av X. Den karakteristiska funktionen för A, definieras nu som
en delmängd av X. Den karakteristiska funktionen för A, definieras nu som
Inom sannolikhetsteorin, och ibland även i andra sammanhang, kallas denna funktion istället för indikatorfunktion, och brukar betecknas 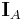 eller
eller 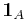 . Detta för att undvika sammanblandning med den karakteristiska funktionen för en stokastisk variabel.
. Detta för att undvika sammanblandning med den karakteristiska funktionen för en stokastisk variabel.
Definition (sannolikhetsteori)
Inom sannolikhetsteorin har, som nämnts ovan, termen karakteristisk funktion en annan betydelse, som kommer av att denna funktion helt karakteriserar sannolikhetsfördelningen för en stokastisk variabel. Med andra ord, om två stokastiska variabler har samma karakteristiska funktion, så har de samma fördelning. För en stokastisk variabel ξ, eller mera allmänt en stokastisk vektor, definieras den karakteristiska funktionen som:
där 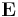 betecknar väntevärde och <,> betecknar skalärprodukt. Man kan också skriva detta som en integral:
betecknar väntevärde och <,> betecknar skalärprodukt. Man kan också skriva detta som en integral:
varefter man noterar att den karakteristiska funktionen är, så när som på ett minustecken i exponenten, fouriertransformen av sannolikhetsmåttet dF. Om ξ har en täthetsfunktion kan vi skriva detta som:
där fξ är täthetsfunktionen för ξ.