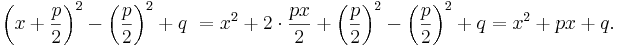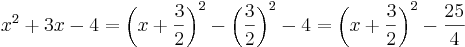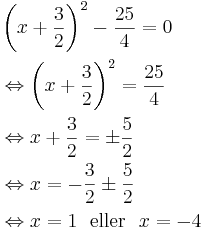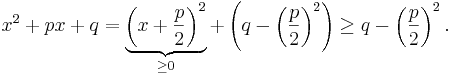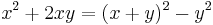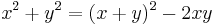Kvadratkomplettering

Från Rilpedia

Version från den 30 mars 2009 kl. 10.27 av Alexbot (Diskussion)
(skillnad) ← Äldre version | Nuvarande version (skillnad) | Nyare version → (skillnad)
Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif

Kvadratkomplettering är att skriva ett andragradspolynom (polynom av grad 2) i kvadratisk form:

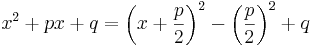x^2 + px + q = \left(x + \frac{p}{2} \right)^2 - \left(\frac{p}{2}\right)^2 + q.

Kvadratkomplettering används bland annat för att lösa andragradsekvationer.

Innehåll

Härledning

Med hjälp av en av kvadreringsreglerna utvecklar vi högerledet i ekvationen ovan och visar att det är lika med ekvationens vänsterled:

\left(x + \frac{p}{2} \right)^2 - \left(\frac{p}{2}\right)^2 + q\ = x^2 + 2 \cdot \frac{px}{2} + \left(\frac{p}{2}\right)^2 - \left(\frac{p}{2}\right)^2 + q = x^2 + px + q.

Exempel

Säg att man vill hitta lösningen till ekvationen x2 + 3x − 4 = 0. Man kan då använda kvadratkomplettering:

x^2 + 3x -4 = \left( x + \frac{3}{2} \right)^2 - \left( \frac{3}{2} \right)^2 - 4 = \left( x + \frac{3}{2} \right)^2 - \frac{25}{4}

sätt ovanstående lika med noll och lös:

\begin{align} &{} \left(x + \frac{3}{2} \right)^2 - \frac{25}{4} = 0 \\ &{} \Leftrightarrow \left(x + \frac{3}{2} \right)^2 = \frac{25}{4} \\ &{} \Leftrightarrow x + \frac{3}{2} = \pm \frac{5}{2} \\ &{} \Leftrightarrow x = - \frac{3}{2} \pm \frac{5}{2} \\ &{} \Leftrightarrow x = 1 ~~ \mathrm{eller} ~~ x = -4 \end{align}

Tillämpning

Med kvadratkomplettering kan man lokalisera andragradspolynomets minsta värde:

x^2 + px + q = \underbrace{\left(x + \frac{p}{2} \right)^2}_{\geq 0} + \left(q - \left(\frac{p}{2}\right)^2\right)\geq q - \left(\frac{p}{2}\right)^2.

Denna olikhet visar att det minsta värdet q − (p / 2)2 antas då talet x är lika med talet − p / 2.

Varianter

Kvadratkomplettering kan även användas på andra sätt, exempelvis för att skriva om följande exempel.

x^2 + 2xy = (x+y)^2 - y^2\,
x^2 + y^2 = (x+y)^2 - 2xy\,

Se även

Hämtad från "https://sv.rilpedia.org/wiki/Kvadratkomplettering"
Personliga verktyg