Polyeder
Från Rilpedia

En polyeder (av grekiskans polys, många, och hedra, yta), begränsas av ett ändligt antal plan och har ett antal månghörningar, polygoner, som sidoytor.
Med en regelbunden polyeder avser man normalt en polyeder där alla begränsningsytor är lika regelbundna polygoner. Det finns precis fem sådana polyedrar, vilket bevisades av Euklides. Dessa kallas platonska kroppar.
Om man även tillåter "inbuktningar", så att polyedern inte är konvex finns fler möjligheter.
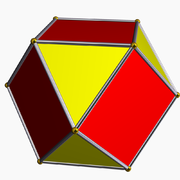
De arkimediska kropparna har regelbundna månghörningar som begränsningsytor, men dessa behöver inte vara lika sinsemellan. Däremot är alla hörn lika. Det finns precis tretton arkimediska kroppar (femton om två "spegelbilder" räknas separat).
Ytterligare polyedrar som består av regelbundna polygoner är regelbundna prismor och regelbundna antiprismor samt de s.k. Johnsons kroppar.
Johnsons kroppar är polyedrar som inte är platonska, arkimediska, prismor eller antiprismor och har sidor som alla är regelbundna månghörningar. Man har visat att det finns 92 sådana polyedrar. En fyrsidig pyramid, med en kvadrat som bas och tre liksidiga trianglar som sidoytor, är exempel på en sådan.
Se även
- polygon (månghörning)
- platonsk kropp