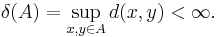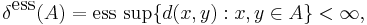Begränsad mängd
Från Rilpedia
En begränsad mängd är inom matematik en mängd där det, intuitivt uttryckt, finns ett största avstånd mellan elementen i mängden som är ändligt. En mängd som inte är begränsad kallas för en obegränsad mängd.
Innehåll |
Mängder av reella tal
En mängd A av reella tal är uppåt begränsad om det finns ett reellt tal M så att 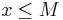 för alla x i A. A kallas nedåt begränsad om det finns ett tal m så att
för alla x i A. A kallas nedåt begränsad om det finns ett tal m så att 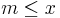 för alla x i A. Om en mängd är både uppåt och nedåt begränsad är det en begränsad mängd, det vill säga om det finns ett tal s så att | x | < s för alla x i A.
för alla x i A. Om en mängd är både uppåt och nedåt begränsad är det en begränsad mängd, det vill säga om det finns ett tal s så att | x | < s för alla x i A.
Likartat, om A är en delmängd till Rn är A begränsad om det finns ett reellt tal s så att | x | < s för alla x i A.
Metriska rum
Om A är en delmängd till ett metriskt rum (X,d), är A begränsad om
δ(A) kallas för mängden A:s diameter. Detta är ekvivalent med att A ryms i någon boll av ändlig radie. Om δ(X) är ändlig, dvs (X,d) är begränsad i sig själv, kalls (X,d) ett begränsat metriskt rum och d kallas en begränsad metrik.
Att en mängd är totalt begränsad implicerar att den är begränsad.
Måttrum
Om A är en delmängd till ett metriskt måttrum (X,d,µ), är A väsentligt begränsad om
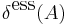 kallas för mängden A:s väsentliga diameter och ess sup är väsentligt supremum med produktmåttet
kallas för mängden A:s väsentliga diameter och ess sup är väsentligt supremum med produktmåttet 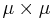 . Måttet µ måste vara ett sigma-begränsat mått.
. Måttet µ måste vara ett sigma-begränsat mått.
Ordningsteori
En lattice sägs vara begränsad om det innehåller både ett största och minsta element. En lattice 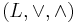 är begränsad om och endast om det finns ett neutralt element med avseende på både
är begränsad om och endast om det finns ett neutralt element med avseende på både 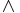 och
och 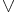 .
.
Referenser
- Persson, Arne; Lars-Christer Böiers: Analys i flera variabler, Studentlitteratur, 2005. ISBN 91-44-03869-0.
- Kreyszig, Erwin: Introductory Functional Analysis, John Wiley & Sons, 1978. ISBN 0-471-50731-8.
- Svensson, Per-Anders: Abstrakt algebra, Studentlitteratur, 2001. ISBN 91-44-01262-4.