Differentierbarhet

Från Rilpedia

Version från den 29 mars 2009 kl. 15.30 av Moberg (Diskussion)
(skillnad) ← Äldre version | Nuvarande version (skillnad) | Nyare version → (skillnad)
Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif

Differentierbarhet, en lokal egenskap hos en funktion som generaliserar begreppet deriverbarhet. Ur differentierbarhet följer kontinuitet och kedjeregeln. Den senare är användbar i den matematiska analysens tillämpningar.

Definition

Funktionen 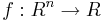f:R^n \rightarrow R säges vara differentierbar i punkten 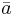\bar{a} omm

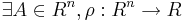\exists A \in R^n, \rho:R^n \rightarrow R sådana att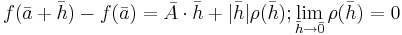 f( \bar{a} + \bar{h} ) - f(\bar{a}) = \bar{A} \cdot \bar{h} + |\bar{h}| \rho(\bar{h}); \lim_{\bar{h} \rightarrow \bar{0}} \rho(\bar{h}) = 0

En funktion säges vara differentierbar på en mängd M om funktionen är differentierbar i alla punkter i M. Det kan observeras att definitionen av differentierbarhet är ekvivalent med definitionen för deriverbarhet då n = 1. För vektorvärda funktioner betraktas komponentfunktionernas differentierbarhet.

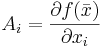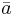Man kan visa A_i =\frac{ \partial f(\bar{x})}{\partial x_i} liksom att existensen av kontinuerliga partiella derivator för en funktion implicerar differentierbarhet. Liksom ekvationen för tangenten till funktionen kan utläsas ur defintionen av deriverbarhet beskriver högerledet i definitionen ovan tangentplanet till funktionen i punkten \bar{a}.

Se även


Lebesgue Icon.svg Denna artikel om matematisk analys är bara påbörjad. Du kan hjälpa till genom att utöka den.
Hämtad från "https://sv.rilpedia.org/wiki/Differentierbarhet"
Personliga verktyg
På andra språk