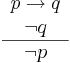Satslogik
Från Rilpedia
| Logik, Formellt system |
|---|
| Logiska system |
| Satslogiska härledningsregler |
|---|
Satslogik avser allmänt studiet av de resonemang som kan föras med språkliga satser som satts samman av mindre satser med språkelement som icke, och, eller, om... så..., om och endast om etcetera; dessa är så kallade konnektiv.
Ofta är de minsta beståndsdelarna i satserna så kallade atomära satser, eller elementarsatser, vilka man vanligtvis betecknar med en bokstav. Vanliga bokstäver är p till t. Man tänker sig att dessa bokstäver står för meningsfulla satser.
Mycket vanligt i satslogik är att man i utsagorna får veta att av det ena följer det andra, en så kallad implikation. En implikation är ett uttryck som beskriver ett logiskt förhållande mellan de ingående satserna. Implikationen är endast falsk om p (förledet) är sant och q (efterledet) falskt. En implikation betecknas med en så kallad implikationspil →, och betyder "om... så...".
Exempel på satslogiska påståenden
- p = "Det regnar"
- q = "Jag är sur"
- ¬p = "Det regnar inte".
- p
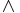 q = "Det regnar och jag är sur".
q = "Det regnar och jag är sur". - p
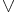 q = "Antingen regnar det, eller så är jag sur" (eller båda).
q = "Antingen regnar det, eller så är jag sur" (eller båda). - p → q = "Om det regnar, så är jag sur".
- p ↔ q = "Det regnar om och endast om jag är sur" (måste gälla åt båda håll).
Härledning
I satslogiken studeras regler som är logiskt giltiga, vilket innebär att om premisserna (det som antas) är sanna så är slutsatsen sann. Ett exempel på en logisk regel är Modus tollens, som tillämpas på följande sätt:
Detta kan förtås på följande sätt. Vi använder samma beteckningar som tidigare, det vill säga p står för "det regnar" och q står för "jag är sur". Satsen "det regnar inte", är alltså sann under förutsättningarna att "om det regnar, så är jag sur" är sann och "jag är inte sur" är sann. Om man accepterat att "om det regnar, så är jag sur" är en sann sats, så måste man därmed, om man accepterar att "jag är inte sur" är sann, acceptera att också "det regnar inte" är sann. Detta kräver inte att man tror att man kan styra vädret med sitt humör, eftersom tolkningen av implikation inte har något att göra med kausalitet, utan bara att satsen "det regnar inte" måste vara sann vid alla tillfällen då satsen "jag är inte sur" är sann.