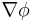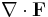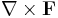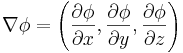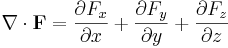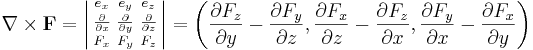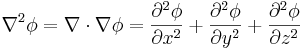Nablaoperatorn

Från Rilpedia

Version från den 18 oktober 2008 kl. 20.53 av Calle (Diskussion)

(skillnad) ← Äldre version | Nuvarande version (skillnad) | Nyare version → (skillnad)

Hoppa till: navigering, sök

Texten från svenska Wikipedia

Inom vektoranalysen är nablaoperatorn en differentialoperator betecknad med symbolen 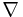$\nabla$ . Symbolen är ett kortare och bekvämare tecken för den vektorlika operatorn (i tre dimensioner med kartesiska koordinater):

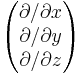
$\begin{pmatrix} {\partial / \partial x} \\ {\partial / \partial y} \\ {\partial / \partial z} \end{pmatrix}$

Symbolen introducerades av William Rowan Hamilton. Namnet nabla kommer från ett hebreiskt stränginstrument med liknande form.

Operatorn kan appliceras på skalärfält ( $φ$ ) eller vektorfält (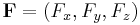 $\mathbf{F} = (F_x,F_y,F_z)$ ), för att ge:

Gradient: $\nabla \phi$
Divergens: $\nabla \cdot \mathbf{F}$
Rotation: $\nabla \times \mathbf{F}$

$\nabla \phi = \left(\frac{\partial \phi}{\partial x},\frac{\partial \phi}{\partial y},\frac{\partial \phi}{\partial z}\right)$
$\nabla \cdot \mathbf{F} = \frac{\partial F_x}{\partial x} + \frac{\partial F_y}{\partial y} + \frac{\partial F_z}{\partial z}$
$\nabla \times \mathbf{F} = \left\vert\begin{smallmatrix}e_x & e_y & e_z \\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y}&\frac{\partial}{\partial z} \\ F_x & F_y & F_z\end{smallmatrix}\right\vert = \left(\frac{\partial F_z}{\partial y} - \frac{\partial F_y}{\partial z}, \frac{\partial F_x}{\partial z} - \frac{\partial F_z}{\partial x},\frac{\partial F_y}{\partial x} - \frac{\partial F_x}{\partial y} \right)$

Om man kombinerar gradient och divergens får man Laplaceoperatorn, vilken betecknas med nablaoperatorn i kvadrat, 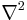$\nabla^2$ :

$\nabla^2 \phi = \nabla \cdot \nabla \phi = \frac{\partial^2 \phi}{\partial x^2} + \frac{\partial^2\phi}{\partial y^2} + \frac{\partial^2 \phi}{\partial z^2}$

Samt för vektorfält: 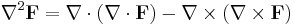$\nabla^2 \mathbf{F} = \nabla \cdot (\nabla \cdot \mathbf{F}) - \nabla \times (\nabla \times \mathbf{F})$

Räkneregler

Genom att tolka nablaoperatorn som en vektor och använda räkneregler för vektorprodukter kan man visa följande räknerregler för nablaoperatorn.

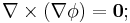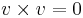$\nabla \times (\nabla \phi) = \mathbf{0};$ För varje vektor v gäller det att den vektoriella produkten $v \times v = 0$ .

Se även

Nablaoperatorn

Från Rilpedia

Räkneregler

Se även

Visningar

Personliga verktyg

Sök

Navigering

Bibeln

Övrigt

Verktygslåda

På andra språk