Glatt funktion

Från Rilpedia

Texten från svenska Wikipedia

En glatt funktion (även kallad slät funktion) är en funktion som är oändligt många gånger deriverbar. Mängden av alla glatta funktioner brukar betecknas med .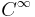

Komplexa funktioner är släta omm de är en gång deriverbara. (De är till och med analytiska).

Exempel

• Alla polynom är oändligt deriverbara.
• e^x är oändligt deriverbar med avseende på x.
• sin x och cos x är oändligt deriverbara.
• Funktionen som definieras av f(x)=x^2 då x>0 och f(x)=-x^2 så x<0 är kontinuerligt deriverbar, men inte slät eftersom dess derivata inte är deriverbar.

Se även

• kontinuerlig funktion
• analytisk funktion

• glatt kurva
• glatt yta

 Denna artikel om matematisk analys är bara påbörjad. Du kan hjälpa till genom att utöka den.