Ortogonalitet

Från Rilpedia

Texten från svenska Wikipedia

Ortogonalitet är i matematiken en egenskap hos par av bland annat vektorer och funktioner. Det är detsamma som att den inre produkten mellan dem är lika med noll. Ofta skrivs 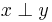för att beteckna att 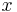och 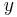är ortogonala.

Ortogonalitet i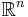

Att två vektorer x och y är ortogonala definieras som att den inre produkten är lika med noll: .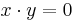

Ortogonalitet är, i fallet då båda vektorerna är skilda från nollvektorn, detsamma som rätvinklighet.

Ortogonalitet i funktionsrum

Att två funktioner f(x) och g(x) är ortogonala på intervallet [a,b] definieras som att den inre produkten är lika med noll:

.

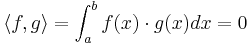Exempelvis är sinus och cosinus ortogonala mot varandra på [0,2π].