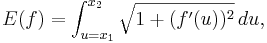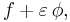Från Rilpedia

Kortfattat kan man säga att variationskalkyl behandlar problemet att bestämma det minsta värdet av en funktional, E(f), som beror av funktion, f. Genom att sätta in olika funktioner f får man olika värden på funktionalen E(f). Problemet handlar om att finna den funktion f som ger det minsta värdet hos E(f).

Skillnaden mellan variationskalkyl och vanlig kalkyl ligger i det att man inom variationskalkyl varierar en funktion, f, medan man inom vanlig kalkyl varierar ett tal och söker efter det tal x som ger det minsta värdet hos en funktion g(x).

Ett viktigt problem som man kan lösa med hjälp av variationskalkyl är problemet att bestämma det kortaste avståndet, E(f), mellan två fixerade punkter; Symbolen f betecknar en funktion som går genom de fixerade punkterna. En viktig sak att notera är vilken mängd de två punkterna i fråga tillhör:

• Om de ligger i det tredimensionella rummet är det kortaste avståndet den räta linje som sammanbinder punkterna.
• Om de ligger på ett klot är det kortaste avståndet en storcirkelbåge som sammanbinder punkterna.

För att matematiskt formulera variationsproblemet då de fixerade punkterna, x = (x₁,x₂) och y = (y₁,y₂) , ligger i planet 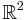låter vi 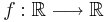vara en funktion som går genom de två punkterna: f(x₁) = x₂ och f(y₁) = y₂. Längden E(f) hos funktionens graf ges då av följande integral:

där symbolen 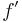betecknar derivatan av funktionen f. Genom att variera funktionen f får vi olika värden på längden E(f). Vi vill se vad som händer med längden då vi tar funktionskurvor som ligger nära funktionskurvan f. Ett sätt att göra detta på är att ersätta f med funktionen

där 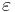är ett litet positivt tal och 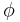en godtyckligt vald funktion som låter sig deriveras hur många gånger som helst.