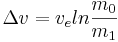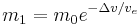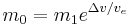Tsiolkovskijs raketekvation
Från Rilpedia
Tsiolkovskijs raketekvation, uppkallad efter Konstantin Tsiolkovskij som var en av flera som självständigt formulerade ekvationen, behandlar funktionen hos en raket: en farkost som kan accelerera sig själv genom att stöta ifrån sig delar av sin egen massa (reaktionsmassa) i hög fart i motsatt håll.
Raketekvationen lyder som följer: för varje raketmanöver, eller sekvens av raketmanövrar gäller:
eller
som är likvärdigt med:
där m0 är den ursprungliga massan, m1 är massan efter manövern/manövrarna, och ve är hastigheten hos raketens avgas i relation till raketen.
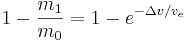 är den del av ursprungsmassan som används som reaktionsmassa.
är den del av ursprungsmassan som används som reaktionsmassa.
Historik
Raketekvationen härleddes självständigt av Konstantin Tsiolkovskij mot slutet av 1800-talet och är allmänt förknippad med hans namn. Dock visar en nyligen upptäckt pamflett "A Treatise on the Motion of Rockets" av William Moore[1] att den tidigaste kända härledningen gjordes 1813 vid Royal Military Academy i Woolwich i England. Ekvationen tillämpades då för vapenforskning.
Referenser
- ↑ Johnson W., "Contents and commentary on William Moore's a treatise on the motion of rockets and an essay on naval gunnery", International Journal of Impact Engineering, band 16, nummer 3, juni 1995, sid. 499-521