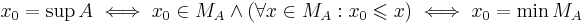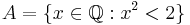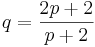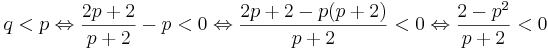Supremum
Från Rilpedia
Supremum innebär minsta övre gräns och är inom matematiken något som är applicerbart på mängder. Det är en generalisering av maximum som även inbegriper mängder utan något största värde, som till exempel ett öppet intervall. Minsta övre gräns kallas ibland även minsta majorant. Supremum av en mängd A betecknas 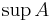 , eller
, eller 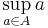 .
.
En vanlig generalisering av supremum till godtyckliga delmängder av 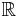 ges av att man låter
ges av att man låter 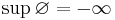 (där
(där 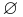 är den tomma mängden),
är den tomma mängden), 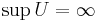 , för en uppåt obegränsad mängd U.
, för en uppåt obegränsad mängd U.
Den analoga generaliseringen av minimum kallas infimum.
Formell definition
Formellt kan man skriva det som, för en mängd 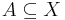 , med linjär ordning
, med linjär ordning 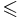 :
:
Låt 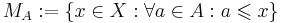 . Då gäller
. Då gäller
(Där minimumet existerar precis då supremumet gör det)
Supremumegenskapen
Man säger att en ordnad mängd S har supremumegenskapen om varje icketom uppåt begränsad delmängd till S har ett supremum (som också ligger i S).
De naturliga talen (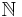 ) och de reella talen (
) och de reella talen (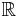 ) har supremumegenskapen. En mängd som inte har supremumegenskapen är de rationella talen (
) har supremumegenskapen. En mängd som inte har supremumegenskapen är de rationella talen (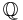 ). Ett exempel på en delmängd i
). Ett exempel på en delmängd i 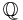 som inte har ett supremum är:
som inte har ett supremum är:
Dvs, alla tal vars kvadrat är mindre än 2. Att hitta ett rationellt supremum till den här mängden är omöjligt. Det är lätt att hitta en övre gräns, vilket positivt tal vars kvadrat är större än 2 går bra. Säg nu att man väljer ett rationellt tal som är en övre gräns. Då kan det omöjligtvis vara den minsta översta gränsen, då 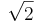 är ett irrationellt tal. Man kan då, oberoende av vilket rationellt tal man valt som övre gräns, alltid hitta ett mindre rationellt tal som också är övre gräns. Detta kan visas mer strikt genom att man antar att man har en godtycklig övre gräns för A, kallad p och p2 > 2. Då är även följande q en övre gräns till A:
är ett irrationellt tal. Man kan då, oberoende av vilket rationellt tal man valt som övre gräns, alltid hitta ett mindre rationellt tal som också är övre gräns. Detta kan visas mer strikt genom att man antar att man har en godtycklig övre gräns för A, kallad p och p2 > 2. Då är även följande q en övre gräns till A:
Vilket är sant då p2 > 2. För att se att q är en övre gräns:
Då p2 > 2 är 2p2 − 4 > 2 * 2 − 4 = 0. Alltså är q en övre gräns till A som är mindre än p.
Referenser
- Walter Rudin, Principles of Mathematical Analysis, Third Edition, McGraw-Hill, 1976.