Stel kropp
Från Rilpedia

En stel kropp är inom klassisk mekanik en kropp som ej kan deformeras. Trots att det inte finns något material vari stela kroppar kan realiseras, är begreppet mycket användbart, speciellt som en modell för kroppar vars deformation är försumbar. Detta beror till stor del på att beskrivning och analys av mekaniken hos en stel kropp är avsevärt förenklad jämfört med mekaniken hos en flexibel eller deformabel kropp. Rörelsen hos stela kroppar studeras inom området stela kroppars dynamik.
I hållfasthetsläran kan en stel kropp beskrivas som att den har oändlig elasticitetsmodul.
Stela kroppars dynamik
Klassisk mekanik innehåller ett specialområde som beskriver translationer och rotationer för stela kroppar. På 1700-talet gav Leonhard Euler detaljerade analyser av allmänna fall.
Fria kroppar
För en fri kropp kan rörelserna beskrivas som en vektorsumma av en uniform translation av kroppens masscentrum och uniforma rotationer kring masscentrum. Att masscentrum av en fri kropp utför en uniform rätlinjig rörelse beror på rörelsemängdens bevarande.
Rörelsemängdsmoment är också bevarad och det ger att även rotationerna är uniforma, det vill säga att de har konstant vinkelhastighet. Stela kroppars rotationsrörelser kan ändå se komplicerade ut på grund av att rotationer kring olika axlar inte nödvändigtvis har samma perioder. Dessa rörelser har studerats av Louis Poinsot (1777 - 1859).
Externa krafter och vridmoment
För externa vridmoment av allmän form är Eulers ekvationer svåra att lösa. Ekvationerna blir något enklare när det finns cylindersymmetri, som i snurror och gyroskop. Vridmoment ger där precession av rotationsaxeln.
När rotationen sker längs en fast axel, kan man bortse från vinkelhastighetens vektorkaraktär. I sådana fall har sambanden för rotation en stor likhet med formlerna för rätlinjiga rörelser.
| Translation | Rotation | |
|---|---|---|
| Hastighet, vinkelhastighet | 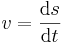 |
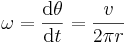 |
| Kinetisk energi | 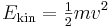 |
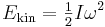 |
| Rörselsemängd(-smoment) | 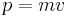 |
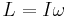 |
| Kraft, vridmoment | 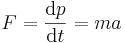 |
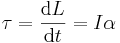 |



