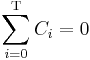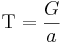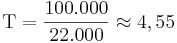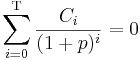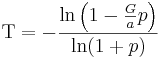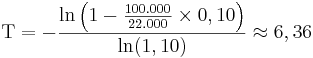Från Rilpedia

Payback-metoden, pay off-metoden eller återbetalningsmetoden är en metod som används för att räkna ut hur snabbt en investering betalar sig själv. Metoden kan antingen användas för att kontrollera att en investering lönar sig inom rimlig tid, eller för att jämföra vilket av flera investeringsalternativ som är bäst.

Payback tid, pay off tid eller återbetalningstid är dess resultat; den tid som krävs för att investeringen ska ge tillbaka investeringskostnaden.

Innehåll 1 Översikt 1.1 Exempel 1 2 Den diskonterade payback metoden 2.1 Exempel 2 3 Beslutsregler 4 Se även 5 Referenser 5.1  Fotnoter 5.2 Tryckta källor 5.3 Webbkällor 6 Externa länkar

Översikt

Payback-metoden var tidigare mer känd som pay off-metoden, men då payback metoden har blivit det vanligare uttrycket i svenskan under senare år används det i denna artikel. I modern engelsk litteratur används uteslutande uttrycket payback. Den svenska varianten återbetalningsmetoden kan emellanåt användas, men det är ytterst ovanligt.

Metoden används ofta vid enklare investeringskalkyler, för grovsållning, eller när investeringskostnaden är väldigt stor. Den är lämpligast vid industriella investeringar, som ofta kan vara mer beroende av svårbedömda framtida faktorer som prisnivåer och konkurrenssituation. Det är den vanligaste kalkyleringsmetoden hos tillverkande företag^[1].

Det är den enda metod inom investeringskalkylering som, åtminstone i sin grundform, inte tar hänsyn till någon kalkylränta. Det handlar om enkel addition, där inbetalningsöverskotten (inbetalningarna minus utbetalningarna) i tur och ordning adderas till den negativa grundinvesteringen till dess att summan är minst noll.

Matematiskt kan det (förenklat) uttryckas som lösningen på följande ekvation:

T är payback tiden, C_i är varje inbetalning eller utbetalning, inklusive grundinvesteringen, fram till att resultatet är noll. Övriga matematiska symboler på denna sida förklaras i artikeln investeringskalkylering.

Om alla inbetalningsöverskott är lika stora, går det att beräkna direkt: grundinvestering (G) dividerat med årligt inbetalningsöverskott (a).

Notera att denna formel kan ge återbetalningstider i delar av år. Om alla inbetalningar sker i slutet av året, måste resultatet avrundas uppåt.

Exempel 1

Om en investering kostar 100.000 kronor att genomföra, och sedan återbetalar 22.000 kronor om året i åtta år, kan beräkningen se ut så här:

	G	a
	År 0	År 1	År 2	År 3	År 4	År 5	År 6	År 7	År 8
Betalningar:	-100.000	22.000	22.000	22.000	22.000	22.000	22.000	22.000	22.000
Ackumulerat:	-100.000	-78.000	-56.000	-34.000	-12.000	10.000	32.000	54.000	76.000

Payback tiden är då maximalt 5 år. Om inbetalningsöverskotten är jämnt fördelade över året, kan vi interpolera den till cirka 4,5 år. Den direkta beräkningen för konstanta inbetalningsöverskott skulle ge:

Om inbetalningarna kommer i slutet av året, avrundas det uppåt till 5 år.

Den diskonterade payback metoden

Det förekommer att paybacktiden beräknas med hänsyn till kalkylräntan (p). Beloppen måste då diskonteras till nuvärden, innan additionen genomförs. Den generella formeln blir då:

För konstanta inbetalningsöverskott blir den:

Funktionen ln är den naturliga logaritmen, log_e.

Exempel 2

Följande tabell beskriver samma exempel som ovan, med 10% kalkylränta:

	G	a
	År 0	År 1	År 2	År 3	År 4	År 5	År 6	År 7	År 8
Betalningar:	-100.000	22.000	22.000	22.000	22.000	22.000	22.000	22.000	22.000
Nuvärden:	-100.000	20.000	18.182	16.529	15.026	13.660	12.418	11.289	10.263
Ackumulerat:	-100.000	-80.000	-61.818	-45.289	-30.263	-16.603	-4.184	7.105	17.368

Det tar maximalt 7 år. Vi kan interpolera det till cirka 6,4 år. Använder vi formeln för fasta belopp, får vi:

Beslutsregler

• En investering som betalar sig själv inom investeringens ekonomiska livslängd är lönsam.
• Vid jämförelser är som regel det alternativ som har kortast återbetalningstid som är mest ekonomiskt fördelaktig.

Se även

• Investeringskalkylering
• Nuvärdemetoden

Referenser

 Fotnoter

1. ↑ Hur vanliga olika kalkyleringsmetoder är bekräftas bland annat av en C-uppsats på Karlstads Universitet, som även går igenom tidigare undersökningar i frågan. Uppsatsen behandlar dock endast industriella investeringar i företag. Finansiella investeringar för företag, privatpersoner och organisationer behandlas inte. Se vidare Persson, Karin; Gustaf Posse, Maria Rosner: Investeringsbedömning - En studie om investeringsbedömningen i ett antal svenska tillverkande företag, Karlstads Universitet, Karlstad 2007 (PDF) (svenska). Hämtat 14 juni 2008. 

Tryckta källor

• Andersson, Göran: Kalkyler som beslutsunderlag, Studentlitteratur, Lund [1983] 2001, 5:e uppl. (svenska). ISBN 91-44-01910-6. 

Webbkällor

• Paul Björnsson. ”Investeringsbedömning” (på sv) (PDF). Institutionen för teknisk ekonomi och logistik, Lunds Tekniska Högskola. http://www.iml.lth.se/kurser/mio201/Material/Investeringar/F1oF2_Inv.PDF. Läst 1 juni 2008. 

Externa länkar

• Beskrivning av hur man beräknar payback tiden i Microsoft Excel och OpenOffice.org