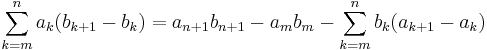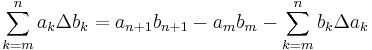Partiell summation

Från Rilpedia

Texten från svenska Wikipedia

Partiell summation är inom matematik en formel för att omvandla summor av produkter till en ofta mer lätthanterlig form. Formeln kallas ibland för Abels lemma eller Abeltransformation och kan liknas med partiell integration.

Formel

Om $(a k)$ och $(b k)$ är talföljder så är

$\sum_{k=m}^n a_k(b_{k+1}-b_k) = a_{n+1}b_{n+1}-a_mb_m - \sum_{k=m}^n b_k(a_{k+1}-a_k)$

Detta kan uttryckas mer kompakt med framåtdifferensoperatorn $Δ$ :

$\sum_{k=m}^n a_k \Delta b_k = a_{n+1}b_{n+1}-a_mb_m - \sum_{k=m}^n b_k \Delta a_k$

Partiell summation

Från Rilpedia

Formel

Visningar

Personliga verktyg

Sök

Navigering

Bibeln

Övrigt

Verktygslåda

På andra språk