Pappos' sats

Från Rilpedia

Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif
Pappostheorem.png

Pappos' sats är en sats i geometrin. Den är uppkallad efter den grekiske matematikern Pappos, som bevisade satsen första gången omkring år 300. Satsen säger följande:

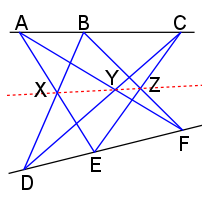
Låt A, B och C vara punkter på en linje och D, E och F vara punkter på en annan linje. Då ligger skärningspunkterna X, Y och Z mellan linjerna AE och DB, AF och DC respektive BF och EC på en linje.

Pascals sats är en generalisering av Pappos sats.


Nuvola apps kpovmodeler.svg Denna artikel om geometri är bara påbörjad. Du kan hjälpa till genom att utöka den.
Hämtad från "https://sv.rilpedia.org/wiki/Pappos%27_sats"
Personliga verktyg