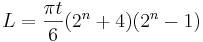Från Rilpedia

Konsten att vika papper, eller origami, har studerats ur matematisk synvikel sedan länge. Områden för studier är bland annat modellernas förmåga att plattas ut i ett plan, och användandet av pappersvikning för att lösa matematiska ekvationer.

Några klassiska geometriska konstruktionsproblem, till exempel vinkelns tredelning och kubens fördubbling har bevisats omöjliga att lösa med endast passare och linjal, men kan lösas med några få pappersvikningar. Med pappersvikning kan man lösa ekvationer upp till grad 4. (Huzitas axiom är ett viktigt bidrag till detta område av matematiken).

Genom att tillämpa geometriska principer vid origami har metoder som Hagas teorem gjort det möjligt att dela in en kvadrats sidor i tre, fem, sju och nio lika delar. Andra teorem och metoder har gjort det möjligt att konstruera andra former från en kvadrat, såsom liksidiga trianglar, femhörningar och sexhörningar och speciella rektanglar som gyllene rektangeln och liknande.

Rigid origami där man undersöker problematiken kring vikning av styva, icke tänjbara, material som t.ex. plåt, och där varje veck antas uppföra sig som om ytorna på båda sidor om vecket var ihopfogade med gångjärn, har stor praktisk betydelse. Så har t.ex. Miura-kartvikning använts för att vika ihop de solpaneler som användes i vissa satelliter.

Längden som krävs på ett papper för att kunna vika det n gånger ges av formeln

där t är papperets tjocklek (angivet i samma enhet som längden L). Denna formel togs fram av Britney Gallivan år 2001 (hon gick då fortfarande i high school), i samband med att hon lyckades vika ett papper 12 gånger. Det hade tidigare länge ansetts omöjligt att vika något, oavsett tjocklek, mer än åtta gånger.

Pappret Britney Gallivan vek 2001 va toalettpapper och hon vek pappret från kortända till kortända, Dock har Mythbusters testat myten att man inte kan vika ett papper mer en 7 gånger genom att vika det på hälften sen vida det 90 grader och vika det på hälften igen dom skalade upp ett A4 uppskattat till en fotbollspan i en NASA hangar och vek pappret 11 gånger

Referenser

Artikeln är, helt eller delvis, en översättning från engelskspråkiga Wikipedia.

Externa länkar

• Origami Mathematics Page av Dr. Tom Hull
• Rigid Origami av Dr. Tom Hull
• Origami & Math av Eric M. Andersen
• Paper Folding Geometry på cut-the-knot
• Dividing a Segment into Equal Parts by Paper Folding på cut-the-knot
• Britney Gallivan has solved the Paper Folding Problem
• Folding Paper - Great Moments in Science - ABC